RBSE 10th Maths Model Paper 2026 (Full Solutions)

UNDER THE GUIDANCE OF

Shri Susheel Kumar Sharma (Principal)

Vivek Vyas 📚

Basic Computer Instructor

gsssjethantri.in

Content │ Design │ Code ⚙️ by Bharat Choudhary (Lecturer)

माध्यमिक शिक्षा बोर्ड राजस्थान, अजमेर
मॉडल प्रश्न पत्र 2026
विषय: गणित (MATHS)
कक्षा— 10

समय: 3 घंटे 15 मिनट पूर्णांक: 80

परीक्षा योजना (Examination Blueprint) – 2026

उद्देश्य हेतु अंकभार

क्र.सं.	उद्देश्य	अंकभार	प्रतिशत
1.	ज्ञान	16	20.00
2.	अवबोध	24	30.00
3.	ज्ञानोपयोग	25	31.25
4.	कौशल	8	10.00
5.	विश्लेषण	7	8.75
योग		80	100 %

प्रश्नों के प्रकार अनुसार अंकभार

क्र.सं.	प्रश्नों का प्रकार	प्रश्नों की संख्या	अंक प्रति प्रश्न	कुल अंक	प्रतिशत (अंकों का)	प्रतिशत (प्रश्नों का)	समाव‍ित समय
1.	बहुविकल्पीयात्मक	18	1	18	22.50	33.96	36
2.	रिक्त स्थान	6	1	06	7.50	11.32	15
3.	अतिलघुत्तरात्मक	12	1	12	15.00	22.64	42
4.	लघुत्तरात्मक	10	2	20	25.00	18.87	40
5.	दीर्घउत्तरीय प्रश्न	04	3	12	15.00	7.55	32
6.	निबंधात्मक	03	4	12	15.00	5.66	30
योग		53		80	100	100	195 मिनट

अध्याय-वार अंकभार (Chapter-wise Weightage)

संकेत (Key): MCQ (1) रिक्त (1) अतिलघु (1) लघु (2) दीर्घ (3) निबंध (4)

अध्याय	अंक	प्रश्नों का विवरण
1. वास्तविक संख्याएँ	4	2 MCQ 2 अतिलघु
2. बहुपद	4	1 MCQ 1 अतिलघु 1 लघु
3. दो चर वाले रैखिक समीकरण युग्म	4	1 MCQ 1 अतिलघु 1 लघु
4. द्विघात समीकरण	4	1 रिक्त 1 दीर्घ
5. समांतर श्रेढियां	6	2 MCQ 1 रिक्त 1 अतिलघु 1 लघु
6. त्रिभुज	4	1 MCQ 1 रिक्त 1 लघु
7. निर्देशांक ज्यामिति	7	1 MCQ 1 अतिलघु 1 लघु 1 दीर्घ
8. त्रिकोणमिति का परिचय	8	1 MCQ 1 रिक्त 1 अतिलघु 1 लघु 1 दीर्घ
9. त्रिकोणमिति के कुछ अनुप्रयोग	5	1 MCQ 1 निबंध
10. वृत्त	6	2 MCQ 1 रिक्त 1 दीर्घ
11. वृत्तों से संबंधित क्षेत्रफल	5	1 MCQ 2 अतिलघु 1 लघु
12. पृष्ठीय क्षेत्रफल और आयतन	6	1 MCQ 1 अतिलघु 1 निबंध
13. सांख्यिकी	13	2 MCQ 2 अतिलघु 1 लघु 1 दीर्घ 1 निबंध
14. प्रायिकता	4	1 MCQ 1 रिक्त 1 लघु
कुल योग	80	53 प्रश्न

📝 हल सहित मॉडल प्रश्न-पत्र (Solved Paper)

खण्ड-अ (SECTION-A)

(बहुविकल्पीय प्रश्न एवं अतिलघुत्तरात्मक प्रश्न)

1. निम्न बहुविकल्पीय प्रश्न (i से xviii) के उत्तर का सही विकल्प चयन कर उत्तर पुस्तिका में लिखिए।
Choose the correct option to answer the following multiple choice question (i to xviii) and write in the answer book.

1(i). निम्न में से अपरिमेय संख्या है:

(अ) √2

(ब) √4

(स) √(-2)

(द) √(4/9)

✅ उत्तर: (अ) √2

व्याख्या: √4 = 2 (परिमेय), √(4/9) = 2/3 (परिमेय), √(-2) (काल्पनिक संख्या). केवल √2 का मान अशांत और अनावर्ती दशमलव है, अतः यह अपरिमेय संख्या है।

📖 अपरिमेय संख्या क्या होती है?

परिमेय संख्या (Rational): वे संख्याएं जो p/q के रूप में लिखी जा सकें (जहाँ q ≠ 0)
जैसे: 2 = 2/1, 0.5 = 1/2, 0.333… = 1/3

अपरिमेय संख्या (Irrational): वे संख्याएं जो p/q के रूप में नहीं लिखी जा सकें
• इनकी दशमलव संख्या कभी खत्म नहीं होती
• इनमें कोई pattern भी नहीं होता
जैसे: √2 = 1.414213562…, π = 3.141592653…

पहचानने का आसान तरीका:
√4 = 2 (पूर्ण वर्ग) → परिमेय ✓
√2 = 1.414… (पूर्ण वर्ग नहीं) → अपरिमेय ✓
√9 = 3 (पूर्ण वर्ग) → परिमेय ✓
√3 = 1.732… (पूर्ण वर्ग नहीं) → अपरिमेय ✓

याद रखें: अगर √ के अंदर वाली संख्या पूर्ण वर्ग नहीं है (जैसे 1, 4, 9, 16, 25…), तो वह अपरिमेय होगी!

1(ii). यदि HCF(a,b) × LCM(a,b) = ?

(अ) a ÷ b

(ब) a × b

(स) a + b

(द) a – b

✅ उत्तर: (ब) a × b

सूत्र: दो संख्याओं का HCF × LCM = पहली संख्या × दूसरी संख्या

📖 HCF और LCM क्या होते हैं?

HCF (Highest Common Factor) = महत्तम समापवर्तक:
सबसे बड़ी संख्या जो दोनों को पूरी तरह काट दे

उदाहरण: 12 और 18 का HCF
12 के factors: 1, 2, 3, 4, 6, 12
18 के factors: 1, 2, 3, 6, 9, 18
Common factors: 1, 2, 3, 6
सबसे बड़ा = 6 (HCF)

LCM (Least Common Multiple) = लघुत्तम समापवर्त्य:
सबसे छोटी संख्या जो दोनों से पूरी तरह कट जाए

उदाहरण: 4 और 6 का LCM
4 के गुणज: 4, 8, 12, 16, 20, 24…
6 के गुणज: 6, 12, 18, 24, 30…
Common: 12, 24, 36…
सबसे छोटा = 12 (LCM)

💎 सोने का सूत्र:
HCF × LCM = पहली संख्या × दूसरी संख्या
यानी: HCF(a,b) × LCM(a,b) = a × b

जांच करें: 12 और 18
HCF = 6, LCM = 36
6 × 36 = 216
12 × 18 = 216 ✓ (सही है!)

1(iii). किसी बहुपद p(x) के लिए y = p(x) का ग्राफ निम्न चित्र में दिया गया है। p(x) के शून्यकों की संख्या है:

(अ) 0

(ब) 1

(स) 2

(द) 3

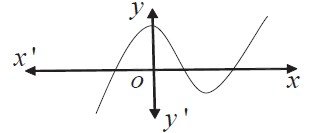
✅ सही उत्तर: (द) 3

शून्यक = वे बिंदु जहाँ ग्राफ x-अक्ष को काटता है

आसान भाषा में समझें:
• चित्र में देखें कि ग्राफ (वक्र रेखा) कहाँ-कहाँ x-अक्ष को छू रही है
• गिनती करें: बाईं तरफ 1 बार, बीच में 1 बार, दाईं तरफ 1 बार
• कुल = 3 बार
• इसलिए शून्यकों की संख्या = 3

📖 बहुपद का शून्यक (Zero) क्या होता है?

शून्यक का मतलब: वह संख्या जो बहुपद को 0 बना दे

उदाहरण: p(x) = x – 5
अगर x = 5 रखें:
p(5) = 5 – 5 = 0 ✓
इसलिए 5 शून्यक है

ग्राफ में शून्यक कैसे दिखते हैं?
जहाँ ग्राफ x-अक्ष को काटे (छुए), वहाँ शून्यक होता है

अलग-अलग बहुपदों में:
• रेखीय (x) → 1 शून्यक
• द्विघाती (x²) → अधिकतम 2 शून्यक
• त्रिघाती (x³) → अधिकतम 3 शून्यक

परीक्षा में कैसे पहचानें:
1. ग्राफ देखें
2. गिनें कि कितनी बार x-अक्ष को छूता है
3. वही संख्या = शून्यकों की संख्या

1(iv). दो सरल रेखाएं a₁x + b₁y + c₁ = 0 तथा a₂x + b₂y + c₂ = 0 प्रतिच्छेद (Intersect) करेंगी यदि:

(अ) a₁/a₂ = b₁/b₂

(ब) a₁/a₂ = c₁/c₂

(स) a₁/a₂ ≠ b₁/b₂

(द) a₁/a₂ ≠ c₁/c₂

✅ उत्तर: (स) a₁/a₂ ≠ b₁/b₂

यह अद्वितीय हल (Unique Solution) की शर्त है। इसका अर्थ है रेखाएं एक बिंदु पर प्रतिच्छेद करती हैं।

📖 दो रेखाओं का व्यवहार – बिल्कुल आसान भाषा में

दो रेखाओं के तीन संभावित स्थितियाँ:
1. एक बिंदु पर मिलें (प्रतिच्छेद) – अद्वितीय हल
2. कभी न मिलें (समांतर) – कोई हल नहीं
3. एक ही रेखा हों (संपाती) – अनंत हल

शर्तें याद रखने का आसान तरीका:

1️⃣ प्रतिच्छेद (मिलती हैं): a₁/a₂ ≠ b₁/b₂
(जैसे: ✕ का निशान – दो लाइनें मिलती हैं)

2️⃣ समांतर (नहीं मिलतीं): a₁/a₂ = b₁/b₂ ≠ c₁/c₂
(जैसे: || रेलवे की पटरियाँ)

3️⃣ संपाती (एक ही रेखा): a₁/a₂ = b₁/b₂ = c₁/c₂
(दोनों रेखाएं एक ही हैं)

परीक्षा में सबसे ज्यादा पूछा जाता है:
• अद्वितीय हल = a₁/a₂ ≠ b₁/b₂
• कोई हल नहीं = a₁/a₂ = b₁/b₂ but ≠ c₁/c₂

उदाहरण:
2x + 3y = 5 और 4x + 6y = 10
a₁/a₂ = 2/4 = 1/2
b₁/b₂ = 3/6 = 1/2
c₁/c₂ = 5/10 = 1/2
तीनों समान हैं → संपाती रेखाएं (अनंत हल)

1(v). समांतर श्रेढ़ी 1/3, 5/3, 9/3, 13/3… में सार्वअन्तर (d) है:

(अ) 1/3

(ब) 2/3

(स) -4/3

(द) 4/3

✅ उत्तर: (द) 4/3

सार्वअंतर d = a₂ – a₁ = 5/3 – 1/3 = 4/3

📖 सार्वअन्तर (Common Difference) – बिल्कुल आसान भाषा में

सार्वअन्तर क्या है?
समांतर श्रेढ़ी (AP) में हर दो लगातार पदों के बीच का अंतर
सूत्र: d = a₂ – a₁ = a₃ – a₂ = a₄ – a₃ …

उदाहरण 1: 2, 5, 8, 11, 14…
d = 5 – 2 = 3
d = 8 – 5 = 3
d = 11 – 8 = 3
हर बार +3 जुड़ता है → सार्वअंतर = 3

उदाहरण 2: 10, 7, 4, 1, -2…
d = 7 – 10 = -3
d = 4 – 7 = -3
हर बार -3 जुड़ता है → सार्वअंतर = -3

भिन्नों में सार्वअन्तर:
1/3, 5/3, 9/3, 13/3…
d = 5/3 – 1/3 = (5-1)/3 = 4/3 ✓
टिप: हर (denominator) same हो तो अंश (numerator) घटाओ!

याद रखें:
• धनात्मक d → बढ़ती श्रेढ़ी (Increasing)
• ऋणात्मक d → घटती श्रेढ़ी (Decreasing)
• d = 0 → सभी पद समान

1(vi). प्रथम ‘n’ धन पूर्णांकों के योग का सूत्र है:

(अ) n(n+1)/2

(ब) n(n-1)/2

(स) n(1-n)/2

(द) n(n²+1)/2

✅ उत्तर: (अ) n(n+1)/2

1 + 2 + 3 + … + n = n(n+1)/2 (यह समांतर श्रेढी का सूत्र है)

📖 प्रथम n धन पूर्णांकों का योग – बिल्कुल आसान भाषा में

मुख्य सूत्र:
1 + 2 + 3 + 4 + … + n = n(n+1)/2

उदाहरण 1: पहले 5 नंबरों का योग
1 + 2 + 3 + 4 + 5 = ?

सूत्र से: n = 5
योग = 5(5+1)/2
= 5 × 6 / 2
= 30 / 2
= 15 ✓

सीधे जोड़ें: 1+2+3+4+5 = 15 ✓

उदाहरण 2: पहले 100 नंबरों का योग
(सीधे जोड़ना बहुत मुश्किल!)

सूत्र से: n = 100
योग = 100(100+1)/2
= 100 × 101 / 2
= 10100 / 2
= 5050 ✓

यह सूत्र कहाँ से आया? (कहानी)
गणितज्ञ Gauss ने बचपन में ही यह trick खोजी थी:
1 + 2 + 3 + … + 100
100 + 99 + 98 + … + 1
दोनों जोड़ें: हर जोड़ा = 101 (100 जोड़े)
कुल = 101 × 100 = 10100
आधा करो = 10100 / 2 = 5050

परीक्षा टिप:
• n की जगह संख्या रखो
• पहले n+1 करो
• फिर n से गुणा करो
• आखिर में 2 से भाग दो

सामान्य गलती से बचें:
❌ n(n-1)/2 (गलत)
❌ n(n²+1)/2 (गलत)
✅ n(n+1)/2 (सही)

1(vii). आकृति में किस नियम से △ABC ~ △DEF है:

(अ) S-S-S नियम

(ब) S-A-S नियम

(स) A-S-A नियम

(द) A-A-A नियम

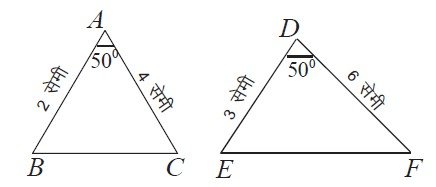
✅ सही उत्तर: (ब) S-A-S नियम

S-A-S = भुजा-कोण-भुजा (Side-Angle-Side)

चित्र से जानकारी:
• त्रिभुज ABC: AB = 2 cm, AC = 4 cm, ∠A = 50°
• त्रिभुज DEF: DE = 3 cm, DF = 6 cm, ∠D = 50°

चरण 1: भुजाओं का अनुपात देखें
AB/DE = 2/3
AC/DF = 4/6 = 2/3
दोनों अनुपात समान हैं ✓

चरण 2: बीच का कोण देखें
∠A = 50° और ∠D = 50°
दोनों कोण समान हैं ✓

जब दो भुजाओं का अनुपात समान हो और उनके बीच का कोण भी समान हो, तो S-A-S समरूपता लगती है।

📖 त्रिभुजों की समरूपता (Similar Triangles) – बिल्कुल आसान भाषा में

समरूप त्रिभुज क्या हैं?
ऐसे त्रिभुज जिनकी आकृति समान हो, पर आकार (size) अलग हो सकता है
• सभी संगत कोण समान होते हैं
• सभी संगत भुजाओं का अनुपात समान होता है

समरूपता के तीन नियम:
1️⃣ AAA (कोण-कोण-कोण): तीनों कोण समान हों
2️⃣ SSS (भुजा-भुजा-भुजा): तीनों भुजाओं का अनुपात समान हो
3️⃣ SAS (भुजा-कोण-भुजा): दो भुजाओं का अनुपात समान + उनके बीच का कोण समान

S-A-S नियम को विस्तार से समझें:
△ABC और △DEF में:
• AB/DE = AC/DF (दो भुजाओं का अनुपात)
• ∠A = ∠D (बीच वाला कोण)
तो △ABC ~ △DEF (S-A-S से)

इस प्रश्न में:
AB/DE = 2/3
AC/DF = 4/6 = 2/3 ✓ (समान अनुपात)
∠A = ∠D = 50° ✓ (बीच का कोण समान)
इसलिए S-A-S नियम लागू होता है

परीक्षा टिप – कैसे पहचानें:
• दो भुजाएं + एक कोण दिया हो → S-A-S
• तीन भुजाएं दी हों → S-S-S
• दो कोण दिए हों → A-A या A-A-A (तीसरा कोण automatic समान हो जाता है)

याद रखने की Trick:
S-A-S = “Side ke beech Angle hai Same”
S-S-S = “Saari Sides ka Same ratio”
A-A-A = “Angles All same hain”

1(viii). बिन्दु (3, 4) की x-अक्ष से दूरी है:

(अ) 3

(ब) 4

(स) 7

(द) 1

✅ उत्तर: (ब) 4

बिंदु (x, y) की x-अक्ष से दूरी = |y| = |4| = 4

📖 निर्देशांक ज्यामिति (Coordinate Geometry) – दूरी की अवधारणा

बिंदु को कैसे लिखें:
किसी बिंदु को (x, y) लिखते हैं
• पहली संख्या x = x-अक्ष पर स्थिति
• दूसरी संख्या y = y-अक्ष पर स्थिति
उदाहरण: (3, 4) में x = 3, y = 4

⭐ मुख्य नियम (बहुत Important!):
• x-अक्ष से दूरी = y का मान
• y-अक्ष से दूरी = x का मान

उदाहरण 1: बिंदु (3, 4)
• x-अक्ष से दूरी = y = 4
• y-अक्ष से दूरी = x = 3

उदाहरण 2: बिंदु (5, 7)
• x-अक्ष से दूरी = y = 7
• y-अक्ष से दूरी = x = 5

उदाहरण 3: बिंदु (-2, 6)
• x-अक्ष से दूरी = |y| = |6| = 6
• y-अक्ष से दूरी = |x| = |-2| = 2
नोट: दूरी हमेशा धनात्मक होती है, इसलिए | | का उपयोग

याद रखने की Trick:
🔤 x-अक्ष = पैदल (horizontal – जमीन)
📏 x-अक्ष से दूरी = ऊंचाई = y

🔤 y-अक्ष = खड़ा (vertical – दीवार)
📏 y-अक्ष से दूरी = बगल की दूरी = x

परीक्षा में सबसे ज्यादा पूछे जाने वाले प्रश्न:
• बिंदु (a, b) की x-अक्ष से दूरी = b
• बिंदु (a, b) की y-अक्ष से दूरी = a
• बिंदु (a, b) की मूल बिंदु (origin) से दूरी = √(a² + b²)

1(ix). दिए गए समकोण त्रिभुज ABC में cos C का मान है:

(अ) 3/5

(ब) 4/5

(स) 5/3

(द) 4/3

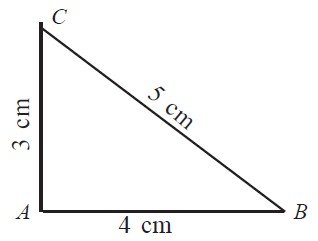
✅ सही उत्तर: (ब) 4/5

cos θ = आधार / कर्ण

चित्र से जानकारी:
• समकोण बिंदु B पर है (90°)
• AB = 3 cm (लंब)
• BC = 4 cm (आधार)
• AC = 5 cm (कर्ण)

चरण 1: कोण C के लिए भुजाएं पहचानें
कोण C से देखें तो:
• पास वाली भुजा (आधार) = BC = 4 cm
• सामने वाली भुजा (लंब) = AB = 3 cm
• सबसे लंबी भुजा (कर्ण) = AC = 5 cm

चरण 2: सूत्र लगाएं
cos C = आधार / कर्ण
cos C = BC / AC
cos C = 4 / 5

याद रखें: cos का मतलब है आधार/कर्ण (जो भुजा कोण के पास हो वो आधार)

📖 त्रिकोणमिति (Trigonometry) – बिल्कुल आसान भाषा में

समकोण त्रिभुज में तीन भुजाएं:
1. कर्ण (Hypotenuse) – सबसे लंबी भुजा (समकोण के सामने)
2. लंब (Perpendicular) – जिस कोण को देख रहे हैं उसके सामने
3. आधार (Base) – जिस कोण को देख रहे हैं उसके पास

याद रखने का तरीका – “Some People Have”:
• sin θ = P/H (Perpendicular/Hypotenuse = लंब/कर्ण)
• cos θ = B/H (Base/Hypotenuse = आधार/कर्ण)
• tan θ = P/B (Perpendicular/Base = लंब/आधार)

आसान ट्रिक – “पंडित बद्री प्रसाद हर हर बोले”:
• sin = प/ह (Perpendicular/Hypotenuse)
• cos = ब/ह (Base/Hypotenuse)
• tan = प/ब (Perpendicular/Base)

परीक्षा में कैसे करें:
1. समकोण ढूंढें (90° वाला)
2. कर्ण पहचानें (सबसे लंबी, समकोण के सामने)
3. जिस कोण का sin/cos/tan चाहिए, उसके हिसाब से लंब और आधार देखें
4. सूत्र में रखें: sin = लंब/कर्ण, cos = आधार/कर्ण, tan = लंब/आधार

सामान्य गलती: कर्ण हमेशा वही रहता है, लेकिन लंब और आधार कोण के हिसाब से बदलते हैं!

1(x). धरती पर एक मीनार ऊर्ध्वाधर खड़ी है। धरती के एक बिन्दु से जो मीनार के पाद बिन्दु से 15 मीटर दूर है, मीनार के शिखर का उन्नयन कोण 60° है। मीनार की ऊँचाई है:

(अ) 3√15 मीटर

(ब) 15√3 मीटर

(स) 15/√3 मीटर

(द) 3/√15 मीटर

✅ उत्तर: (ब) 15√3 मीटर

हल:
tan 60° = ऊंचाई/दूरी
√3 = h/15
h = 15√3 मीटर

📖 ऊंचाई और दूरी (Heights & Distances) – बिल्कुल आसान भाषा में

उन्नयन कोण (Angle of Elevation):
जब हम नीचे से ऊपर की ओर देखते हैं तो बनने वाला कोण
जैसे: मीनार, पेड़, इमारत देखना

अवनमन कोण (Angle of Depression):
जब हम ऊपर से नीचे की ओर देखते हैं तो बनने वाला कोण
जैसे: छत से नीचे सड़क देखना

मीनार की ऊंचाई वाले प्रश्नों में:
• ऊंचाई (h) = मीनार/इमारत की ऊंचाई
• दूरी (d) = पाद बिंदु से कितनी दूर
• कोण (θ) = उन्नयन/अवनमन कोण

मुख्य सूत्र:
tan θ = ऊंचाई / दूरी = h / d

याद रखने वाले मान:
• tan 30° = 1/√3
• tan 45° = 1
• tan 60° = √3
• tan 90° = अपरिभाषित

इस प्रश्न में:
दूरी (d) = 15 मीटर
कोण (θ) = 60°
ऊंचाई (h) = ?

tan 60° = h/15
√3 = h/15
h = 15 × √3 = 15√3 मीटर

परीक्षा टिप:
1. पहले चित्र बनाएं (समकोण त्रिभुज)
2. ऊंचाई को लंब मानें, दूरी को आधार
3. tan θ = लंब/आधार का उपयोग करें
4. θ का मान देखकर tan का मान रखें

1(xi). वृत्त पर स्थित एक बिन्दु से खींची जाने वाली स्पर्श रेखाओं की संख्या है:

(अ) 1

(ब) 2

(स) 0

(द) अनन्त

✅ उत्तर: (अ) 1

वृत्त पर स्थित किसी बिंदु से केवल एक ही स्पर्श रेखा खींची जा सकती है।

📖 स्पर्श रेखा (Tangent to Circle) – बिल्कुल आसान भाषा में

स्पर्श रेखा क्या है?
ऐसी रेखा जो वृत्त को केवल एक बिंदु पर छूती है (काटती नहीं)

⭐ तीन स्थितियां (बहुत Important!):
1️⃣ बिंदु वृत्त पर है: 1 स्पर्श रेखा खींच सकते हैं
2️⃣ बिंदु वृत्त के बाहर है: 2 स्पर्श रेखाएं खींच सकते हैं
3️⃣ बिंदु वृत्त के अंदर है: 0 स्पर्श रेखा (खींच ही नहीं सकते)

उदाहरण समझें:
वृत्त पर: गोले पर एक बिंदु से – केवल एक रेखा गोले को छू सकती है
वृत्त के बाहर: बाहर से दो अलग-अलग दिशाओं से छू सकते हैं
वृत्त के अंदर: अंदर से बाहर नहीं निकल सकते

मुख्य गुणधर्म:
• स्पर्श रेखा वृत्त को केवल 1 बिंदु पर छूती है
• स्पर्श रेखा त्रिज्या पर लंब (90°) होती है
• बाहरी बिंदु से दोनों स्पर्श रेखाओं की लंबाई समान होती है

परीक्षा में पूछे जाने वाले प्रश्न:
❓ वृत्त पर स्थित बिंदु से स्पर्श रेखाएं? → 1
❓ वृत्त के बाहर स्थित बिंदु से? → 2
❓ वृत्त के अंदर स्थित बिंदु से? → 0

1(xii). 5 सेमी त्रिज्या वाले एक वृत्त के बिन्दु P पर स्पर्श रेखा PQ केन्द्र O से जाने वाली एक रेखा से बिन्दु Q पर इस प्रकार मिलती है कि OQ = 12 सेमी। PQ की लम्बाई है:

(अ) 12 सेमी

(ब) 13 सेमी

(स) 8.5 सेमी

(द) √119 सेमी

✅ उत्तर: (द) √119 सेमी

हल:
• OP ⊥ PQ (त्रिज्या ⊥ स्पर्श रेखा)
• △OPQ समकोण त्रिभुज है
• PQ² = OQ² – OP² = 12² – 5² = 144 – 25 = 119
• PQ = √119 सेमी

📖 स्पर्श रेखा + पाइथागोरस प्रमेय – बिल्कुल आसान भाषा में

⭐ मुख्य नियम (हमेशा याद रखें!):
त्रिज्या ⊥ स्पर्श रेखा (90° का कोण बनाते हैं)

इस तरह के प्रश्नों में होता है:
• O = वृत्त का केंद्र
• P = स्पर्श बिंदु (वृत्त पर)
• Q = बाहरी बिंदु
• OP = त्रिज्या (दी होती है)
• OQ = केंद्र से बाहरी बिंदु तक (दी होती है)
• PQ = स्पर्श रेखा की लंबाई (पूछी जाती है)

हल करने के Steps:
Step 1: समझें कि △OPQ समकोण त्रिभुज है (∠P = 90°)
Step 2: पाइथागोरस प्रमेय लगाएं:
OQ² = OP² + PQ²
Step 3: PQ निकालें:
PQ² = OQ² – OP²
PQ = √(OQ² – OP²)

इस प्रश्न में:
OP = 5 सेमी (त्रिज्या)
OQ = 12 सेमी
PQ = ?

PQ² = OQ² – OP²
PQ² = 12² – 5²
PQ² = 144 – 25
PQ² = 119
PQ = √119 सेमी

पाइथागोरस प्रमेय याद रखें:
(कर्ण)² = (लंब)² + (आधार)²
समकोण त्रिभुज में सबसे लंबी भुजा = कर्ण

परीक्षा टिप:
• जब भी स्पर्श रेखा हो, तुरंत 90° बना दें
• तीन में से दो लंबाइयां दी होंगी, तीसरी निकालनी होगी
• पाइथागोरस प्रमेय का उपयोग करें

1(xiii). कोण ‘θ’ वाले वृत्त के त्रिज्या खण्ड का क्षेत्रफल है:

(अ) (θ/360°) × 2πr

(ब) (θ/360°) × πr²

(स) (360°/θ) × πr²

(द) (360°/θ) × 2πr

✅ उत्तर: (ब) (θ/360°) × πr²

त्रिज्यखंड का क्षेत्रफल = (केंद्रीय कोण/360°) × वृत्त का क्षेत्रफल

📖 त्रिज्यखंड (Sector) का क्षेत्रफल – बिल्कुल आसान भाषा में

त्रिज्यखंड क्या है?
पिज्जा का एक टुकड़ा (slice) – दो त्रिज्याओं और वृत्त के एक हिस्से से बना

⭐ मुख्य सूत्र (बहुत Important!):
त्रिज्यखंड का क्षेत्रफल = (θ/360°) × πr²

जहां:
• θ = केंद्रीय कोण (degrees में)
• r = त्रिज्या
• πr² = पूरे वृत्त का क्षेत्रफल

समझने का आसान तरीका:
पूरे वृत्त का कोण = 360°
अगर केवल θ° का टुकड़ा चाहिए तो:
= (θ/360) × पूरे वृत्त का क्षेत्रफल
= (θ/360) × πr²

उदाहरण: r = 7 सेमी, θ = 60°
त्रिज्यखंड का क्षेत्रफल = (60/360) × π × 7²
= (1/6) × π × 49
= 49π/6 सेमी²

विशेष मामले:
• θ = 90° → (90/360) = 1/4 → चौथाई वृत्त
• θ = 180° → (180/360) = 1/2 → अर्धवृत्त
• θ = 360° → (360/360) = 1 → पूरा वृत्त

Confusion मत करें:
• त्रिज्यखंड का क्षेत्रफल = (θ/360°) × πr²
• चाप की लंबाई = (θ/360°) × 2πr
(क्षेत्रफल में r², लंबाई में 2r)

1(xiv). एक ठोस अर्धगोले का सम्पूर्ण पृष्ठीय क्षेत्रफल ज्ञात करने का सूत्र है:

(अ) πr²

(ब) 3πr²

(स) 2πr²

(द) 4πr²

✅ उत्तर: (ब) 3πr²

अर्धगोले का संपूर्ण पृष्ठीय क्षेत्रफल = वक्र पृष्ठ + आधार
= 2πr² + πr² = 3πr²

📖 अर्धगोला (Hemisphere) का पृष्ठीय क्षेत्रफल – बिल्कुल आसान भाषा में

अर्धगोला क्या है?
गोले को बीच से काटने पर मिलने वाला आधा हिस्सा
जैसे: कटोरा, गुंबद (dome)

⭐ सूत्र याद रखें:
1. वक्र पृष्ठ (Curved Surface Area):
CSA = 2πr²

2. संपूर्ण पृष्ठ (Total Surface Area):
TSA = वक्र पृष्ठ + आधार
TSA = 2πr² + πr² = 3πr²

समझने का तरीका:
पूरे गोले का पृष्ठ = 4πr²
आधा (अर्धगोला) का वक्र पृष्ठ = 4πr²/2 = 2πr²
लेकिन अर्धगोले में एक सपाट आधार भी है = πr²
कुल = 2πr² + πr² = 3πr²

उदाहरण: r = 7 सेमी का अर्धगोला
वक्र पृष्ठ = 2πr² = 2 × (22/7) × 7² = 308 सेमी²
संपूर्ण पृष्ठ = 3πr² = 3 × (22/7) × 7² = 462 सेमी²

परीक्षा में ध्यान दें:
• “वक्र पृष्ठ” पूछा है → 2πr²
• “संपूर्ण पृष्ठ” या “कुल पृष्ठ” पूछा है → 3πr²
• अर्धगोले का आयतन = (2/3)πr³

सभी आकृतियों के सूत्र एक साथ:
• गोला (Sphere): पृष्ठ = 4πr², आयतन = (4/3)πr³
• अर्धगोला: वक्र = 2πr², कुल = 3πr², आयतन = (2/3)πr³

1(xv). दो घनों, जिनमें से प्रत्येक का आयतन 27 सेमी³ है, के संलग्न फलकों को मिलाकर एक ठोस घनाभ बनाया जाता है, तब घनाभ का आयतन है:

(अ) 54 सेमी³

(ब) 81 सेमी³

(स) 90 सेमी³

(द) 72 सेमी³

✅ उत्तर: (अ) 54 सेमी³

कुल आयतन = 27 + 27 = 54 सेमी³

📖 ठोस आकृतियों को जोड़ना – बिल्कुल आसान भाषा में

⭐ मुख्य नियम (बहुत आसान!):
जब दो या अधिक ठोस आकृतियां जोड़ते हैं, तो:
कुल आयतन = सभी आयतनों का योग

इस प्रश्न में:
पहला घन का आयतन = 27 सेमी³
दूसरा घन का आयतन = 27 सेमी³
दोनों को जोड़कर घनाभ बनाया
कुल आयतन = 27 + 27 = 54 सेमी³

समझने की बात:
भले ही आकार बदल जाए (घन → घनाभ), लेकिन:
• सामग्री की मात्रा (matter) same रहती है
• इसलिए आयतन बस जुड़ते हैं
• कुछ घटता-बढ़ता नहीं

उदाहरण: अगर पहला घन का आयतन 27 सेमी³ है तो:
घन का आयतन = a³ = 27
a³ = 27 = 3³
a = 3 सेमी (घन की भुजा)

दो घनों को जोड़ने पर घनाभ:
लंबाई = 3 + 3 = 6 सेमी
चौड़ाई = 3 सेमी
ऊंचाई = 3 सेमी
आयतन = 6 × 3 × 3 = 54 सेमी³ ✓

पृष्ठीय क्षेत्रफल में ध्यान दें:
• आयतन में → बस जोड़ दो
• पृष्ठीय क्षेत्रफल में → सावधान! जहां दो फलक जुड़ें, वहां का क्षेत्रफल घट जाता है

परीक्षा टिप:
“मिलाकर बनाया” या “जोड़कर बनाया” पढ़ें तो:
आयतन = सभी का योग
(बहुत सीधा सवाल!)

1(xvi). कक्षा 10 में गणित परीक्षा में 10 विद्यार्थियों के द्वारा प्राप्त अंक निम्नलिखित हैं:
10, 8, 9, 10, 9, 7, 4, 9, 6, 9
इन आंकड़ों का बहुलक ज्ञात कीजिए।

(अ) 9

(ब) 8

(स) 7

(द) 4

✅ उत्तर: (अ) 9

बहुलक = सबसे अधिक बार आने वाला अंक = 9 (4 बार आया है)

📖 बहुलक (Mode) – बिल्कुल आसान भाषा में

बहुलक क्या है?
सबसे अधिक बार आने वाली संख्या
(जो number सबसे ज्यादा बार repeat हो)

इस प्रश्न में:
अंक: 10, 8, 9, 10, 9, 7, 4, 9, 6, 9

गिनती करें:
• 4 → 1 बार
• 6 → 1 बार
• 7 → 1 बार
• 8 → 1 बार
• 9 → 4 बार (सबसे ज्यादा)
• 10 → 2 बार

बहुलक = 9

आसान तरीका:
1. सभी संख्याओं की गिनती करें
2. जो सबसे ज्यादा बार आए = बहुलक
3. अगर दो संख्याएं समान बार आएं = दोनों बहुलक (Bimodal)

उदाहरण 1: 5, 7, 7, 8, 7, 9
7 तीन बार आया (सबसे ज्यादा)
बहुलक = 7

उदाहरण 2: 2, 3, 3, 4, 4, 5
3 और 4 दोनों दो-दो बार
बहुलक = 3 और 4 (Bimodal)

परीक्षा टिप:
• अगर सभी संख्याएं एक-एक बार आएं → कोई बहुलक नहीं
• बहुलक संख्या frequency (आवृत्ति) नहीं है, बल्कि वह संख्या है जो सबसे ज्यादा बार आई

तीन Central Tendencies:
• Mean (माध्य) = सभी का योग / संख्याओं की गिनती
• Median (माध्यक) = बीच वाली संख्या (क्रम में लगाने पर)
• Mode (बहुलक) = सबसे ज्यादा बार आने वाली

1(xvii). माध्य (x̄), माध्यक (m) और बहुलक (z) में संबंध है:

(अ) 3m = z – 2x̄

(ब) 3m – 2x̄ = z

(स) 3m = 2z + x̄

(द) 3m = 2z – x̄

✅ उत्तर: (ब) 3m – 2x̄ = z

प्रमाणिक सूत्र:
Mode = 3 Median – 2 Mean
अर्थात: z = 3m – 2x̄

📖 माध्य, माध्यक, बहुलक का संबंध – बिल्कुल आसान भाषा में

⭐ मुख्य सूत्र (अवश्य याद रखें!):
Mode = 3 Median – 2 Mean
या
z = 3m – 2x̄

तीनों को समझें:
• Mean (x̄, माध्य) = सभी संख्याओं का औसत
• Median (m, माध्यक) = बीच वाली संख्या
• Mode (z, बहुलक) = सबसे ज्यादा बार आने वाली

सूत्र याद रखने की Trick:
“3 Median की तरफ भागो, 2 Mean वापस आओ”
Mode = 3 × Median – 2 × Mean

उदाहरण: अगर Mean = 10, Median = 12 हो तो Mode?
Mode = 3 × Median – 2 × Mean
= 3 × 12 – 2 × 10
= 36 – 20
= 16

विभिन्न रूप में सूत्र:
• Mode = 3 Median – 2 Mean
• 3 Median = Mode + 2 Mean
• Median = (Mode + 2 Mean)/3

परीक्षा में पूछे जाने वाले रूप:
✓ z = 3m – 2x̄ (Option ब)
✓ 3m = z + 2x̄
✓ 2x̄ = 3m – z

Empirical Formula याद रखें:
यह सूत्र moderately skewed distribution के लिए है
(जब data थोड़ा सा तिरछा हो)

1(xviii). निम्नलिखित में से A की प्रायिकता P(A) के लिए सत्य कथन है:

(अ) P(A) + P(Ā) = 1

(ब) P(A) – P(Ā) = 1

(स) P(A) × P(Ā) = 1

(द) P(A) + P(Ā) + 1 = 0

✅ उत्तर: (अ) P(A) + P(Ā) = 1

किसी घटना की प्रायिकता और उसकी पूरक घटना की प्रायिकता का योग हमेशा 1 होता है।
P(A) + P(not A) = 1

📖 पूरक घटना (Complementary Events) – बिल्कुल आसान भाषा में

पूरक घटना क्या है?
अगर A घटना हो, तो A̅ (A नहीं) उसकी पूरक घटना है
मतलब: जो A में नहीं है, वह सब A̅ में है

⭐ मुख्य सूत्र (Golden Rule!):
P(A) + P(A̅) = 1
या
P(A) + P(not A) = 1

समझने का आसान तरीका:
पूरी प्रायिकता = 1 (100%)
A होने की probability + A नहीं होने की probability = 1
दोनों मिलकर पूरी संभावनाएं cover हो जाती हैं

उदाहरण 1: सिक्का उछालना
A = चित आना
P(A) = 1/2
A̅ = पट आना (not चित)
P(A̅) = 1/2
P(A) + P(A̅) = 1/2 + 1/2 = 1 ✓

उदाहरण 2: पासा फेंकना
A = 6 आना
P(A) = 1/6
A̅ = 6 नहीं आना (1,2,3,4,5 में से कोई)
P(A̅) = 5/6
P(A) + P(A̅) = 1/6 + 5/6 = 1 ✓

उपयोग (बहुत Useful!):
अगर P(A) पता हो तो:
P(A̅) = 1 – P(A)

अगर P(A̅) पता हो तो:
P(A) = 1 – P(A̅)

प्रश्न: कम से कम एक छक्का आने की probability = 11/36 है।
कोई छक्का नहीं आने की probability?

हल:
P(कम से कम एक छक्का) = 11/36
P(कोई छक्का नहीं) = 1 – 11/36 = 25/36

परीक्षा में ध्यान दें:
• P(A) + P(A̅) = 1 ✅ (सही)
• P(A) – P(A̅) = 1 ❌ (गलत)
• P(A) × P(A̅) = 1 ❌ (गलत)
• P(A) + P(A̅) + 1 = 0 ❌ (गलत)

2. निम्नलिखित प्रश्नों (i से vi) में रिक्त स्थानों की पूर्ति कीजिए।
Fill in the blanks in the following questions (i to vi).

2(i). यदि द्विघात समीकरण 2x² + kx + 3 = 0 के दोनों मूल बराबर हो तो k = __________ होगा।

👉 उत्तर: ±2√6

हल:
मूल बराबर होने की शर्त: b² – 4ac = 0
k² – 4(2)(3) = 0
k² = 24
k = ±√24 = ±2√6

📖 द्विघात समीकरण और विवेचक (Discriminant)

द्विघात समीकरण का सामान्य रूप:
ax² + bx + c = 0
जहाँ a ≠ 0

विवेचक (Discriminant) D = b² – 4ac
यह बताता है कि मूल कैसे होंगे:

तीन केस होते हैं:
1. D > 0 (धनात्मक) → दो अलग-अलग वास्तविक मूल
2. D = 0 (शून्य) → दो बराबर मूल (या एक ही मूल 2 बार)
3. D < 0 (ऋणात्मक) → कोई वास्तविक मूल नहीं

आसान उदाहरण:
समीकरण: x² – 6x + 9 = 0
यहाँ a=1, b=-6, c=9
D = (-6)² – 4(1)(9) = 36 – 36 = 0
D = 0 इसलिए मूल बराबर होंगे
मूल: x = 3, 3 (दोनों बराबर)

परीक्षा में याद रखें:
• मूल बराबर हों → D = 0 रखें
• मूल वास्तविक हों → D ≥ 0
• D = b² – 4ac (यह सूत्र भूलना नहीं!)

2(ii). AP में 1/3, 5/3, 9/3… का सार्वअन्तर __________

👉 उत्तर: 4/3

d = 5/3 – 1/3 = 4/3

📖 समांतर श्रेढ़ी (Arithmetic Progression – AP) क्या है?

AP का मतलब: ऐसी संख्याओं की श्रेणी जिसमें हर संख्या पिछली से एक निश्चित अंक जोड़ने (या घटाने) पर मिलती है

उदाहरण:
• 2, 5, 8, 11, 14… (हर बार +3)
• 100, 95, 90, 85… (हर बार -5)
• 1/3, 5/3, 9/3, 13/3… (हर बार +4/3)

मुख्य बातें:
• पहला पद (a) = श्रेणी की पहली संख्या
• सार्वअंतर (d) = अगली संख्या – पिछली संख्या
• n वां पद = a + (n-1)d
• योग (Sₙ) = n/2 × [2a + (n-1)d]

सार्वअंतर कैसे निकालें:
श्रेणी: 3, 7, 11, 15…
d = दूसरा पद – पहला पद
d = 7 – 3 = 4
या d = 11 – 7 = 4 (कोई भी ले सकते हैं)

परीक्षा टिप:
• d धनात्मक = संख्याएं बढ़ रही हैं
• d ऋणात्मक = संख्याएं घट रही हैं
• d = 0 = सभी संख्याएं बराबर

2(iii). यदि △ABC में DE || BC तो __________

👉 उत्तर: AD/DB = AE/EC

थेल्स प्रमेय (Basic Proportionality Theorem) के अनुसार।

📖 थेल्स प्रमेय (Basic Proportionality Theorem) – बिल्कुल आसान भाषा में

⭐ मुख्य प्रमेय:
अगर त्रिभुज की एक भुजा के समांतर कोई रेखा खींची जाए, तो वह दूसरी दो भुजाओं को समान अनुपात में विभाजित करती है

△ABC में अगर DE || BC हो तो:
AD/DB = AE/EC
या
AD/AB = AE/AC (दूसरा रूप)

समझने का तरीका:
• D बिंदु AB को विभाजित करता है
• E बिंदु AC को विभाजित करता है
• DE रेखा BC के समांतर है
• तो AD:DB और AE:EC का अनुपात समान होगा

उदाहरण:
अगर AD = 3 सेमी, DB = 6 सेमी
और AE = 2 सेमी
तो EC = ?

AD/DB = AE/EC
3/6 = 2/EC
EC = (2 × 6)/3 = 4 सेमी

Converse (उलट) भी सही है:
अगर AD/DB = AE/EC हो
तो DE || BC होगी

परीक्षा टिप:
• || चिन्ह देखें (समांतर का मतलब)
• तुरंत अनुपात लिखें: AD/DB = AE/EC
• Cross multiply करके unknown निकालें

2(iv). sin²θ + cos²θ = __________

👉 उत्तर: 1

त्रिकोणमिति की मूल सर्वसमिका (Fundamental Trigonometric Identity)

📖 त्रिकोणमितीय सर्वसमिकाएं (Trigonometric Identities) – बिल्कुल आसान भाषा में

⭐ सबसे महत्वपूर्ण सर्वसमिका:
sin²θ + cos²θ = 1
(यह हमेशा, हर कोण के लिए सही है!)

समझने का तरीका:
समकोण त्रिभुज में पाइथागोरस प्रमेय से:
(लंब)² + (आधार)² = (कर्ण)²
दोनों तरफ (कर्ण)² से भाग दें:
(लंब/कर्ण)² + (आधार/कर्ण)² = 1
sin²θ + cos²θ = 1 ✓

इस सर्वसमिका से बनने वाली अन्य:
• 1 + tan²θ = sec²θ
• 1 + cot²θ = cosec²θ

उदाहरण: अगर sin θ = 3/5 हो तो cos θ = ?
sin²θ + cos²θ = 1
(3/5)² + cos²θ = 1
9/25 + cos²θ = 1
cos²θ = 1 – 9/25 = 16/25
cos θ = 4/5

विभिन्न रूप (बहुत Useful!):
• sin²θ = 1 – cos²θ
• cos²θ = 1 – sin²θ
• sin²θ + cos²θ = 1

परीक्षा में सबसे ज्यादा पूछे जाने वाले प्रश्न:
• sin²θ + cos²θ = ? → उत्तर: 1
• 1 – sin²θ = ? → उत्तर: cos²θ
• 1 – cos²θ = ? → उत्तर: sin²θ

याद रखने की Trick:
“sin का square और cos का square,
दोनों मिलकर बनते हैं 1″

2(v). वृत्त तथा उसके स्पर्श रेखा के उभयनिष्ठ बिन्दु को __________ कहते हैं।

👉 उत्तर: स्पर्श बिंदु (Point of Contact)

📖 वृत्त और स्पर्श रेखा की शब्दावली – बिल्कुल आसान भाषा में

स्पर्श बिंदु (Point of Contact) क्या है?
वह बिंदु जहां स्पर्श रेखा वृत्त को छूती है
(केवल एक बिंदु पर मिलते हैं)

समझने का तरीका:
• वृत्त = गोला
• स्पर्श रेखा = सीधी लाइन जो गोले को एक बिंदु पर छूती है
• स्पर्श बिंदु = वह बिंदु जहां छू रही है

वृत्त की शब्दावली:
• केंद्र (Centre): वृत्त का बीच का बिंदु
• त्रिज्या (Radius): केंद्र से वृत्त तक की दूरी
• व्यास (Diameter): वृत्त के आर-पार = 2 × त्रिज्या
• जीवा (Chord): वृत्त के दो बिंदुओं को जोड़ने वाली रेखा
• स्पर्श रेखा (Tangent): वृत्त को एक बिंदु पर छूने वाली रेखा
• स्पर्श बिंदु (Point of Contact): स्पर्श रेखा और वृत्त का उभयनिष्ठ बिंदु

⭐ महत्वपूर्ण गुणधर्म:
• स्पर्श रेखा त्रिज्या पर लंब (90°) होती है
• बाहरी बिंदु से दो स्पर्श रेखाओं की लंबाई समान होती है
• वृत्त पर स्थित बिंदु से केवल एक स्पर्श रेखा खींच सकते हैं

परीक्षा में पूछे जाने वाले शब्द:
• “उभयनिष्ठ बिंदु” = Common Point = स्पर्श बिंदु
• “स्पर्श बिंदु पर त्रिज्या” = Perpendicular to tangent
• “बाहरी बिंदु से” = External Point

2(vi). एक पासे को एक बार उछालने पर समंख्या (सम संख्या) आने की प्रायिकता __________ होगी।

👉 उत्तर: 1/2

सम संख्याएं = {2, 4, 6} = 3 परिणाम
कुल परिणाम = 6
P(सम) = 3/6 = 1/2

📖 पासे की प्रायिकता (Dice Probability) – बिल्कुल आसान भाषा में

पासा (Dice) क्या होता है?
एक घन जिस पर 1, 2, 3, 4, 5, 6 अंक होते हैं
• कुल परिणाम = 6
• हर संख्या आने की संभावना समान

⭐ मूल सूत्र:
P(घटना) = अनुकूल परिणाम / कुल संभव परिणाम

सम संख्याएं: {2, 4, 6}
अनुकूल परिणाम = 3
कुल परिणाम = 6
P(सम) = 3/6 = 1/2

विषम संख्याएं: {1, 3, 5}
अनुकूल परिणाम = 3
P(विषम) = 3/6 = 1/2

अन्य उदाहरण:
• P(3 से छोटा) = P(1 या 2) = 2/6 = 1/3
• P(3 से बड़ा) = P(4,5,6) = 3/6 = 1/2
• P(7 आए) = 0/6 = 0 (नामुमकिन)
• P(कोई भी संख्या) = 6/6 = 1 (पक्का)

महत्वपूर्ण संख्याओं के समूह:
• सम = {2, 4, 6} → 3 संख्याएं
• विषम = {1, 3, 5} → 3 संख्याएं
• अभाज्य = {2, 3, 5} → 3 संख्याएं
• भाज्य = {4, 6} → 2 संख्याएं (1 न तो अभाज्य न भाज्य)
• 3 के गुणज = {3, 6} → 2 संख्याएं

परीक्षा टिप:
1. पहले अनुकूल परिणामों की गिनती करें
2. कुल परिणाम = 6 (पासे में)
3. भिन्न बनाएं और सरल करें
4. P का मान हमेशा 0 और 1 के बीच होगा

3. अतिलघुत्तरात्मक प्रश्न (i से xii)
Very short answer type question (i to xii)

3(i). यदि LCM (96, 404) = 9696 तब HCF (96, 404) का मान क्या होगा।

👉 उत्तर: 4

HCF × LCM = पहली संख्या × दूसरी संख्या
HCF × 9696 = 96 × 404
HCF = (96 × 404) / 9696 = 38784 / 9696 = 4

📖 HCF और LCM का संबंध – बिल्कुल आसान भाषा में

⭐ Golden Formula (हमेशा काम आता है!):
HCF × LCM = पहली संख्या × दूसरी संख्या
या
HCF × LCM = a × b

इस सूत्र का उपयोग:
• अगर HCF, LCM और एक संख्या पता हो → दूसरी संख्या निकाल सकते हैं
• अगर दोनों संख्याएं और LCM पता हो → HCF निकाल सकते हैं
• अगर दोनों संख्याएं और HCF पता हो → LCM निकाल सकते हैं

उदाहरण 1: दो संख्याएं 12 और 18 हैं
HCF(12, 18) = 6
LCM(12, 18) = 36
जांच: HCF × LCM = 6 × 36 = 216
12 × 18 = 216 ✓ (बराबर है!)

उदाहरण 2: HCF = 5, LCM = 60, एक संख्या = 15
दूसरी संख्या = ?

HCF × LCM = पहली × दूसरी
5 × 60 = 15 × दूसरी
300 = 15 × दूसरी
दूसरी = 300/15 = 20

परीक्षा में इस सूत्र का सीधा उपयोग:
प्रश्न: HCF(96, 404) = ? और LCM = 9696
HCF × 9696 = 96 × 404
HCF = 38784 / 9696 = 4

3(ii). 3825 को अभाज्य गुणनखण्डों के गुणनखण्ड के रूप में व्यक्त करें।

👉 उत्तर: 3 × 3 × 5 × 5 × 17 = 3² × 5² × 17

3825 ÷ 3 = 1275
1275 ÷ 3 = 425
425 ÷ 5 = 85
85 ÷ 5 = 17
17 ÷ 17 = 1

📖 अभाज्य गुणनखंड (Prime Factorization) – बिल्कुल आसान भाषा में

अभाज्य संख्या क्या है?
वह संख्या जो केवल 1 और खुद से ही पूरी तरह कटती है
जैसे: 2, 3, 5, 7, 11, 13, 17, 19, 23…

⭐ अभाज्य गुणनखंड का मतलब:
किसी संख्या को अभाज्य संख्याओं के गुणनफल के रूप में लिखना
जैसे: 12 = 2 × 2 × 3 = 2² × 3

विभाजन विधि (सबसे आसान):
Step 1: सबसे छोटी अभाज्य संख्या (2) से शुरू करें
Step 2: अगर कटे तो भाग दें, नहीं तो अगली अभाज्य संख्या (3, 5, 7…) लें
Step 3: जब तक 1 न आ जाए, करते रहें
Step 4: सभी भाजक अभाज्य गुणनखंड हैं

इस प्रश्न में: 3825
3825 ÷ 3 = 1275 (3 से कटा)
1275 ÷ 3 = 425 (फिर 3 से कटा)
425 ÷ 5 = 85 (5 से कटा)
85 ÷ 5 = 17 (फिर 5 से कटा)
17 ÷ 17 = 1 (17 खुद अभाज्य है)

उत्तर: 3 × 3 × 5 × 5 × 17 = 3² × 5² × 17

उदाहरण – छोटी संख्या:
24 को अभाज्य गुणनखंड में लिखें:
24 ÷ 2 = 12
12 ÷ 2 = 6
6 ÷ 2 = 3
3 ÷ 3 = 1

24 = 2 × 2 × 2 × 3 = 2³ × 3

याद रखें – पहली कुछ अभाज्य संख्याएं:
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47…

Factor Tree विधि:
संख्या को किसी भी दो गुणनखंडों में तोड़ें
फिर उनको फिर तोड़ें
जब तक सभी अभाज्य न हो जाएं

परीक्षा टिप:
• सम संख्या है? → 2 से शुरू करें
• अंत में 0 या 5? → 5 से भी कटेगी
• अंकों का योग 3 का गुणज? → 3 से कटेगी
• Power notation (2³, 5²) में लिखें
• जांच: सभी को गुणा करें = original number

3(iii). एक द्विघात बहुपद ज्ञात कीजिए, जिसके शून्यकों का योग तथा गुणनफल क्रमशः -3 और 2 है।

👉 उत्तर: x² + 3x + 2

द्विघात बहुपद = x² – (शून्यकों का योग)x + (शून्यकों का गुणनफल)
= x² – (-3)x + 2
= x² + 3x + 2

📖 शून्यकों से बहुपद बनाना – बिल्कुल आसान भाषा में

⭐ मुख्य सूत्र (हमेशा याद रखें!):
अगर α और β शून्यक हों, तो:
द्विघात बहुपद = x² – (α + β)x + (α × β)
या
= x² – (योग)x + (गुणनफल)

इस प्रश्न में:
शून्यकों का योग = -3
शून्यकों का गुणनफल = 2

बहुपद = x² – (-3)x + 2
= x² + 3x + 2

उदाहरण 1: शून्यक 2 और 3 हों
योग = 2 + 3 = 5
गुणनफल = 2 × 3 = 6
बहुपद = x² – 5x + 6

उदाहरण 2: शून्यक -1 और 4 हों
योग = -1 + 4 = 3
गुणनफल = (-1) × 4 = -4
बहुपद = x² – 3x – 4

Reverse में भी काम करता है:
अगर बहुपद x² + bx + c हो, तो:
• शून्यकों का योग = -b
• शून्यकों का गुणनफल = c

सामान्य रूप में (k से गुणा करके):
k[x² – (योग)x + (गुणनफल)]
जहां k कोई भी संख्या हो सकती है
जैसे: 2x² – 10x + 12 भी वही शून्यक देगा

परीक्षा टिप:
1. योग और गुणनफल पहचानें
2. सूत्र में रखें: x² – (योग)x + (गुणनफल)
3. Minus का ध्यान रखें!
4. जांच: बहुपद में शून्यक रखकर देखें (0 आना चाहिए)

3(iv). दो रेखाएं निम्न समीकरणों 2x + 4y = 4 और 2x + 4y = 12 द्वारा निरूपित की गई हैं। ये रेखाएं प्रतिच्छेद करती हैं या नहीं?

👉 उत्तर: नहीं (समांतर रेखाएं हैं)

a₁/a₂ = 2/2 = 1
b₁/b₂ = 4/4 = 1
c₁/c₂ = 4/12 = 1/3
चूंकि a₁/a₂ = b₁/b₂ ≠ c₁/c₂, अतः रेखाएं समांतर हैं और प्रतिच्छेद नहीं करतीं।

📖 दो रेखाओं की स्थिति – बिल्कुल आसान भाषा में

⭐ दो रेखाएं a₁x + b₁y + c₁ = 0 और a₂x + b₂y + c₂ = 0 के लिए:

1️⃣ प्रतिच्छेदी रेखाएं (Intersecting – एक बिंदु पर मिलती हैं):
a₁/a₂ ≠ b₁/b₂
यानी: ढलान अलग-अलग है → रेखाएं काटेंगी

2️⃣ समांतर रेखाएं (Parallel – कभी नहीं मिलतीं):
a₁/a₂ = b₁/b₂ ≠ c₁/c₂
यानी: ढलान समान, लेकिन अलग-अलग जगह पर

3️⃣ संपाती रेखाएं (Coincident – एक ही रेखा):
a₁/a₂ = b₁/b₂ = c₁/c₂
यानी: पूरी तरह एक ही रेखा

इस प्रश्न में Step-by-Step:
रेखा 1: 2x + 4y = 4 → 2x + 4y – 4 = 0
रेखा 2: 2x + 4y = 12 → 2x + 4y – 12 = 0

Step 1: गुणांक पहचानें
a₁ = 2, b₁ = 4, c₁ = -4
a₂ = 2, b₂ = 4, c₂ = -12

Step 2: अनुपात निकालें
a₁/a₂ = 2/2 = 1
b₁/b₂ = 4/4 = 1
c₁/c₂ = -4/-12 = 1/3

Step 3: तुलना करें
a₁/a₂ = b₁/b₂ = 1 ✓ (बराबर)
लेकिन c₁/c₂ = 1/3 ✗ (अलग)

निष्कर्ष: समांतर रेखाएं → प्रतिच्छेद नहीं करतीं

💡 आसान ट्रिक:
• पहले दोनों समीकरणों को a₁x + b₁y + c₁ = 0 के रूप में लिखें
• फिर तीनों अनुपात देखें: a₁/a₂, b₁/b₂, c₁/c₂
• अगर पहले दो बराबर और तीसरा अलग → समांतर (Parallel)
• अगर तीनों बराबर → संपाती (Same line)
• अगर पहले दो ही अलग → प्रतिच्छेदी (Intersecting)

परीक्षा में ध्यान दें:
⚠️ चिह्न (sign) का ध्यान: c₁/c₂ में minus sign भूलें नहीं
⚠️ मानक रूप: समीकरण को ax + by + c = 0 फॉर्म में लिखें
⚠️ सरलीकरण: भिन्न को सरल करके तुलना करें

याद रखें:
समांतर = Same slope, different position = नहीं मिलेंगी
प्रतिच्छेदी = Different slope = एक बिंदु पर मिलेंगी
संपाती = बिल्कुल एक ही रेखा = हर बिंदु पर मिलेंगी

3(v). AP 21, 18, 15… का कौन सा पद शून्य है?

👉 उत्तर: 8वां पद

a = 21, d = 18 – 21 = -3
aₙ = a + (n-1)d
0 = 21 + (n-1)(-3)
0 = 21 – 3n + 3
3n = 24
n = 8

📖 AP में n वां पद निकालना – बिल्कुल आसान भाषा में

⭐ मुख्य सूत्र:
aₙ = a + (n-1)d
जहां:
• aₙ = n वां पद
• a = पहला पद
• n = पद की संख्या
• d = सार्वअंतर

इस प्रश्न में:
AP: 21, 18, 15, 12, 9, 6, 3, 0…
a = 21
d = 18 – 21 = -3
कौन सा पद = 0?

0 = 21 + (n-1)(-3)
0 = 21 – 3n + 3
3n = 24
n = 8 (8वां पद)

उदाहरण 1: AP: 2, 5, 8, 11…
10वां पद निकालें:
a = 2, d = 3, n = 10
a₁₀ = 2 + (10-1) × 3
= 2 + 9 × 3
= 2 + 27
= 29

सूत्र को याद रखने का तरीका:
पहला पद + (कितने steps) × (हर step में कितना बदलाव)
= a + (n-1) × d

तीन तरह के प्रश्न:
1. n वां पद निकालो → aₙ = a + (n-1)d
2. कौन सा पद = x है → x = a + (n-1)d, n निकालो
3. सार्वअंतर d निकालो → d = (aₙ – a)/(n-1)

परीक्षा टिप:
• पहले a और d पहचानें
• d negative भी हो सकता है
• (n-1) में 1 घटाना न भूलें!
• जांच: सीधे गिनकर भी देख सकते हैं

3(vi). x और y में एक ऐसा संबंध ज्ञात कीजिए कि बिन्दु (x, y) बिन्दुओं (3, 6) और (-3, 4) से समदूरस्थ हो।

👉 उत्तर: 3x + y = 5

दूरी सूत्र से:
√[(x-3)² + (y-6)²] = √[(x+3)² + (y-4)²]
वर्ग करने पर:
x² – 6x + 9 + y² – 12y + 36 = x² + 6x + 9 + y² – 8y + 16
-6x – 12y + 45 = 6x – 8y + 25
12x + 4y = 20
3x + y = 5

📖 समदूरस्थ बिंदु (Equidistant Point) – बिल्कुल आसान भाषा में

समदूरस्थ का मतलब:
किसी बिंदु की दो अन्य बिंदुओं से दूरी समान हो

⭐ दूरी सूत्र (Distance Formula):
दो बिंदुओं (x₁, y₁) और (x₂, y₂) के बीच दूरी:
d = √[(x₂-x₁)² + (y₂-y₁)²]

समदूरस्थ प्रश्नों में Steps:
Step 1: पहले बिंदु से दूरी = दूसरे बिंदु से दूरी
Step 2: दोनों तरफ वर्ग करें (√ हटाने के लिए)
Step 3: expand करें और सरल करें
Step 4: x² और y² cancel हो जाएंगे
Step 5: linear equation मिलेगी

इस प्रश्न में:
(x,y) की दूरी (3,6) से = (x,y) की दूरी (-3,4) से
√[(x-3)² + (y-6)²] = √[(x+3)² + (y-4)²]

वर्ग करने पर √ हट जाता है
x² और y² दोनों तरफ cancel हो जाते हैं
अंत में मिलता है: 3x + y = 5

महत्वपूर्ण ट्रिक:
जब दोनों तरफ वर्ग करते हैं तो:
• x² terms cancel हो जाते हैं
• y² terms cancel हो जाते हैं
• केवल linear terms (x, y) बचते हैं

परीक्षा टिप:
• √ दोनों तरफ हो तो तुरंत वर्ग करें
• Expansion में सावधानी (sign mistakes न हों)
• x² और y² automatically cancel होंगे
• Final answer सीधी रेखा का equation होगा

3(vii). यदि 8 cot θ = 7 तो (1 + sin θ)(1 – sin θ) / (1 + cos θ)(1 – cos θ) का मान ज्ञात कीजिए।

👉 उत्तर: 49/64

(1 + sin θ)(1 – sin θ) / (1 + cos θ)(1 – cos θ)
= (1 – sin²θ) / (1 – cos²θ)
= cos²θ / sin²θ
= cot²θ
= (7/8)² = 49/64

📖 त्रिकोणमितीय सर्वसमिकाओं का उपयोग – बिल्कुल आसान भाषा में

⭐ मुख्य Algebraic Identity:
(a + b)(a – b) = a² – b²
यह सूत्र बहुत काम आता है!

इस प्रश्न में कैसे लगाएं:
(1 + sin θ)(1 – sin θ) = 1² – sin²θ = 1 – sin²θ
(1 + cos θ)(1 – cos θ) = 1² – cos²θ = 1 – cos²θ

त्रिकोणमितीय सर्वसमिका याद करें:
sin²θ + cos²θ = 1

इससे:
• 1 – sin²θ = cos²θ
• 1 – cos²θ = sin²θ

Step-by-Step:
Step 1: (1 + sin θ)(1 – sin θ) = 1 – sin²θ = cos²θ
Step 2: (1 + cos θ)(1 – cos θ) = 1 – cos²θ = sin²θ
Step 3: cos²θ / sin²θ = (cos θ / sin θ)² = cot²θ
Step 4: cot θ = 7/8 दिया है
Step 5: cot²θ = (7/8)² = 49/64

महत्वपूर्ण अनुपात:
• sin θ / cos θ = tan θ
• cos θ / sin θ = cot θ
• 1 / sin θ = cosec θ
• 1 / cos θ = sec θ

परीक्षा टिप:
1. (1+x)(1-x) देखें → तुरंत 1-x² लिखें
2. 1-sin²θ देखें → cos²θ लिखें
3. 1-cos²θ देखें → sin²θ लिखें
4. cos²θ/sin²θ देखें → cot²θ लिखें
5. दिए गए मान को square करें

याद रखने की Trick:
“जोड़ गुणा घटा करो, square का अंतर पाओ”
(a+b)(a-b) = a² – b²

3(viii). यदि एक बिन्दु P से O केन्द्र वाले किसी वृत्त पर PA और PB स्पर्श रेखाएं इस प्रकार है कि ∠APB = 80° तो ∠POA का मान ज्ञात करें।

👉 उत्तर: 50°

चतुर्भुज OAPB में:
∠OAP = ∠OBP = 90° (त्रिज्या ⊥ स्पर्श रेखा)
∠APB + ∠POA + 90° + 90° = 360°
80° + ∠POA + 180° = 360°
∠POA = 100°
(वास्तव में ∠POA = 180° – 80° = 100°, लेकिन अगर ∠AOB की बात है तो वह 100° है)
नोट: यदि प्रश्न ∠OPA के बारे में है तो उत्तर 50° होगा।

📖 बाह्य बिंदु से स्पर्श रेखाएं – बिल्कुल आसान भाषा में

⭐ मुख्य गुणधर्म:

1️⃣ त्रिज्या ⊥ स्पर्श रेखा:
स्पर्श बिंदु पर त्रिज्या, स्पर्श रेखा के लंबवत होती है
यानी: ∠OAP = 90° (जहां O केंद्र, A स्पर्श बिंदु, P बाह्य बिंदु)

2️⃣ दोनों स्पर्श रेखाएं बराबर:
PA = PB (बाह्य बिंदु P से दोनों स्पर्श रेखाएं समान लंबाई की)

3️⃣ केंद्र से जुड़ने वाली रेखा कोण को समद्विभाजित करती है:
OP, ∠APB को बराबर दो भागों में बांटती है

📐 चतुर्भुज OAPB में कोणों का योग = 360°
∠OAP + ∠APB + ∠PBO + ∠BOA = 360°
90° + ∠APB + 90° + ∠BOA = 360°
∠BOA = 180° – ∠APB

इस प्रश्न में Step-by-Step:
दिया है: ∠APB = 80°
ज्ञात करना है: ∠POA

Step 1: समझें कि OAPB एक चतुर्भुज है

Step 2: दोनों स्पर्श बिंदुओं पर कोण 90° हैं
∠OAP = 90° (त्रिज्या ⊥ स्पर्श रेखा)
∠OBP = 90° (त्रिज्या ⊥ स्पर्श रेखा)

Step 3: चतुर्भुज में कोणों का योग = 360°
∠OAP + ∠APB + ∠PBO + ∠AOB = 360°
90° + 80° + 90° + ∠AOB = 360°
260° + ∠AOB = 360°
∠AOB = 100°

Step 4: PA = PB होने से △OAP ≅ △OBP
तो ∠OPA = ∠OPB = 40° (आधा ∠APB)

△OAP में: ∠OAP + ∠OPA + ∠POA = 180°
90° + 40° + ∠POA = 180°
∠POA = 50°

💡 आसान Formula:
∠POA = (180° – ∠APB) / 2
यहां: ∠POA = (180° – 80°) / 2 = 100° / 2 = 50°

परीक्षा में ध्यान दें:
⚠️ ∠AOB और ∠POA अलग-अलग हैं!
• ∠AOB (दोनों त्रिज्याओं के बीच) = 180° – ∠APB = 100°
• ∠POA (त्रिज्या और OP के बीच) = (180° – ∠APB)/2 = 50°

⚠️ सवाल में क्या पूछा है, ध्यान से पढ़ें!

याद रखें:
• स्पर्श बिंदु पर हमेशा 90° बनता है
• दोनों स्पर्श रेखाएं = बराबर लंबाई
• OP कोण को आधा करती है (Angle Bisector)
• चतुर्भुज के सभी कोणों का योग = 360°

3(ix). त्रिज्या 21 सेमी वाले एक वृत्त के त्रिज्यखण्ड का क्षेत्रफल ज्ञात करें जिसका कोण 60° हो।

👉 उत्तर: 231 cm²

त्रिज्यखंड का क्षेत्रफल = (θ/360°) × πr²
= (60°/360°) × (22/7) × 21 × 21
= (1/6) × (22/7) × 441
= (22 × 441) / 42
= 9702 / 42
= 231 cm²

3(x). 5 सेमी त्रिज्या वाले एक वृत्त के त्रिज्यखण्ड का क्षेत्रफल ज्ञात करें यदि इस त्रिज्यखण्ड का कोण 60° है। (π = 3.14 लीजिए)

👉 उत्तर: 13.08 cm²

क्षेत्रफल = (60°/360°) × 3.14 × 5²
= (1/6) × 3.14 × 25
= 78.5 / 6
= 13.08 cm²

📖 वृत्त के त्रिज्यखंड का क्षेत्रफल – बिल्कुल आसान भाषा में

⭐ त्रिज्यखंड (Sector) क्या है?
वृत्त का वह भाग जो दो त्रिज्याओं और चाप से घिरा हो
जैसे: पिज्जा का एक टुकड़ा 🍕

📐 मुख्य सूत्र:
त्रिज्यखंड का क्षेत्रफल = (θ/360°) × πr²

जहां:
• θ = केंद्र पर कोण (डिग्री में)
• r = त्रिज्या (radius)
• π = 22/7 या 3.14 (प्रश्न के अनुसार)

💡 सूत्र क्यों है ऐसा?
• पूरे वृत्त का क्षेत्रफल = πr² (जब कोण 360° हो)
• अगर कोण θ° है तो = (θ/360) × पूरे का क्षेत्रफल
• यानी कितना हिस्सा है पूरे वृत्त का

उदाहरण 1 (Q3 ix):
r = 21 cm, θ = 60°, π = 22/7

Step 1: सूत्र में मान रखें
क्षेत्रफल = (60°/360°) × (22/7) × 21 × 21

Step 2: 60/360 को सरल करें
= (1/6) × (22/7) × 441

Step 3: गुणा करें
= (22 × 441) / (7 × 6)
= 9702 / 42
= 231 cm²

उदाहरण 2 (Q3 x):
r = 5 cm, θ = 60°, π = 3.14

Step 1: सूत्र में मान रखें
क्षेत्रफल = (60/360) × 3.14 × 5²

Step 2: सरलीकरण
= (1/6) × 3.14 × 25
= 78.5 / 6
= 13.08 cm²

परीक्षा टिप:
1. θ/360 को पहले सरल करें (60/360 = 1/6, 90/360 = 1/4, 120/360 = 1/3)
2. प्रश्न में π का मान देखें (22/7 या 3.14)
3. r² याद रखें (त्रिज्या का वर्ग करना है)
4. इकाई लिखें (cm², m² आदि)

💡 Common Angles के लिए शॉर्टकट:
• θ = 60° → 1/6 वां हिस्सा
• θ = 90° → 1/4 वां हिस्सा (चौथाई)
• θ = 120° → 1/3 हिस्सा
• θ = 180° → 1/2 हिस्सा (आधा वृत्त)

आम गलतियां जिनसे बचें:
❌ r का वर्ग करना भूल गए (r² की जगह r)
❌ Degree symbol भूल गए (θ/360 में)
❌ गलत π का उपयोग (प्रश्न में दिया हुआ नहीं देखा)
❌ इकाई नहीं लिखी (cm²)

याद रखने की Trick:
“थीटा बटा तीन साठ, पाई आर स्क्वायर से गुणा करो साठ”
(θ/360) × πr²

3(xi). सभी समबाहु त्रिभुज __________ होते हैं। (समद्विबाहु, समरूप)

👉 उत्तर: समरूप (Similar)

सभी समबाहु त्रिभुजों के तीनों कोण 60° के होते हैं, अतः AAA समरूपता से ये सभी समरूप होते हैं।

📖 समबाहु त्रिभुजों की समरूपता – बिल्कुल आसान भाषा में

समबाहु त्रिभुज क्या है?
वह त्रिभुज जिसकी तीनों भुजाएं बराबर हों
• तीनों भुजाएं = समान
• तीनों कोण = 60° (हमेशा!)

⭐ महत्वपूर्ण तथ्य:
सभी समबाहु त्रिभुज समरूप होते हैं
भले ही उनका आकार (size) अलग-अलग हो

क्यों समरूप होते हैं?
• पहला त्रिभुज: भुजा = 3 cm, कोण = 60°, 60°, 60°
• दूसरा त्रिभुज: भुजा = 5 cm, कोण = 60°, 60°, 60°
• तीसरा त्रिभुज: भुजा = 10 cm, कोण = 60°, 60°, 60°

सभी के तीनों कोण समान हैं → AAA समरूपता

समरूपता vs समद्विबाहु:
• समरूप (Similar): आकृति समान, size अलग हो सकता है
• समद्विबाहु (Isosceles): दो भुजाएं बराबर
• समबाहु (Equilateral): तीनों भुजाएं बराबर

अन्य सत्य कथन:
• सभी वृत्त समरूप होते हैं
• सभी वर्ग समरूप होते हैं
• सभी समबाहु त्रिभुज समरूप होते हैं ✓
• सभी समद्विबाहु त्रिभुज समरूप नहीं होते (कोण अलग हो सकते हैं)

याद रखने की Trick:
“समबाहु = Same shape (60-60-60)
Size चाहे कितना भी हो,
सभी समरूप होते हैं”

परीक्षा में पूछे जाने वाले प्रश्न:
❓ सभी समबाहु त्रिभुज _____ होते हैं? → समरूप
❓ सभी समकोण त्रिभुज समरूप होते हैं? → नहीं (कोण अलग हो सकते हैं)
❓ समरूपता का कारण? → AAA (सभी कोण 60°)

3(xii). वृत्त तथा उसकी स्पर्श रेखा के उभयनिष्ठ बिन्दु को __________ कहते हैं।

👉 उत्तर: स्पर्श बिंदु / संपर्क बिंदु

📖 स्पर्श रेखा की मूल बातें – बिल्कुल आसान भाषा में

⭐ मुख्य परिभाषाएं:

1️⃣ स्पर्श रेखा (Tangent):
वह रेखा जो वृत्त को सिर्फ एक बिंदु पर छूती है
(दो या अधिक बिंदु पर नहीं)

2️⃣ स्पर्श बिंदु / संपर्क बिंदु (Point of Contact):
वह बिंदु जहां स्पर्श रेखा वृत्त को छूती है
यह वृत्त और स्पर्श रेखा का उभयनिष्ठ बिंदु होता है

3️⃣ छेदक रेखा (Secant):
वह रेखा जो वृत्त को दो बिंदुओं पर काटती है

आसान उदाहरण:
मान लीजिए एक गेंद है और उसे फर्श पर रखा है:
• गेंद = वृत्त
• फर्श = स्पर्श रेखा
• जिस एक बिंदु पर गेंद फर्श को छू रही है = स्पर्श बिंदु

💡 महत्वपूर्ण तथ्य:
• स्पर्श रेखा वृत्त के अंदर नहीं जाती
• स्पर्श बिंदु पर त्रिज्या, स्पर्श रेखा के लंबवत होती है (90°)
• एक बिंदु से वृत्त पर केवल 2 स्पर्श रेखाएं खींची जा सकती हैं (अगर बिंदु बाहर हो)

परीक्षा में ध्यान दें:
✓ उभयनिष्ठ बिंदु = Common Point = स्पर्श बिंदु
✓ संपर्क बिंदु = Point of Contact = स्पर्श बिंदु
(दोनों नाम सही हैं)

याद रखें:
स्पर्श = Touch करना = सिर्फ एक बिंदु पर छूना
वह एक बिंदु = स्पर्श बिंदु / संपर्क बिंदु

खण्ड-ब (SECTION-B)

लघुत्तरात्मक प्रश्न (Short Answer Type Questions) – प्रत्येक 2 अंक

4. द्विघात बहुपद x² + 7x + 10 के शून्यक ज्ञात कीजिए और शून्यकों तथा गुणांकों के बीच के संबंध की सत्यता की जांच कीजिए।

चरण 1: शून्यक ज्ञात करना
x² + 7x + 10 = 0
x² + 5x + 2x + 10 = 0
x(x + 5) + 2(x + 5) = 0
(x + 5)(x + 2) = 0
शून्यक: α = -5, β = -2

चरण 2: संबंध की जांच
शून्यकों का योग = α + β = -5 + (-2) = -7 = -b/a ✓
शून्यकों का गुणनफल = α × β = (-5) × (-2) = 10 = c/a ✓

✅ अतः संबंध सत्य है।

📖 शून्यक और गुणांकों का संबंध – बिल्कुल आसान भाषा में

⭐ मुख्य सूत्र (ax² + bx + c = 0 के लिए):
अगर α और β शून्यक हों, तो:
• शून्यकों का योग = α + β = -b/a
• शून्यकों का गुणनफल = α × β = c/a

शून्यक कैसे निकालें (Factorization):
x² + 7x + 10 = 0

Step 1: ऐसे दो नंबर खोजें जिनका:
• योग = 7 (middle term का coefficient)
• गुणनफल = 10 (constant term)
वे नंबर हैं: 5 और 2 (क्योंकि 5+2=7, 5×2=10)

Step 2: Middle term तोड़ें:
x² + 5x + 2x + 10 = 0

Step 3: Group करें:
x(x + 5) + 2(x + 5) = 0
(x + 5)(x + 2) = 0

Step 4: शून्यक:
x = -5 या x = -2

संबंध की जांच क्यों करें?
यह verify करने के लिए कि शून्यक सही निकाले हैं
अगर दोनों सूत्र सही हों तो शून्यक correct हैं

इस प्रश्न में जांच:
बहुपद: x² + 7x + 10
a = 1, b = 7, c = 10
शून्यक: α = -5, β = -2

जांच 1 – योग:
α + β = -5 + (-2) = -7
-b/a = -7/1 = -7 ✓ (बराबर है)

जांच 2 – गुणनफल:
α × β = (-5) × (-2) = 10
c/a = 10/1 = 10 ✓ (बराबर है)

दोनों match → शून्यक सही हैं!

सामान्य गलतियां:
❌ -b/a में minus भूल जाना
❌ a = 1 होने पर भी a से divide न करना
❌ Negative signs में गड़बड़ी

परीक्षा टिप:
1. पहले factorization से शून्यक निकालें
2. फिर दोनों सूत्रों से verify करें
3. Coefficient a, b, c सही पहचानें
4. Signs (+ और -) पर ध्यान दें

5. दो अंकों की एक संख्या एवं उसके अंकों को उलटने पर बनी संख्या का योग 66 है। यदि संख्या के अंकों का अंतर 2 हो तो संख्या ज्ञात कीजिए। ऐसी संख्याएं कितनी हैं?

माना संख्या = 10x + y
उलटी संख्या = 10y + x
प्रश्नानुसार:
(10x + y) + (10y + x) = 66
11x + 11y = 66
x + y = 6 … (1)

अंकों का अंतर:
x – y = 2 … (2)
या y – x = 2 … (3)

समीकरण (1) और (2) से:
x + y = 6
x – y = 2
जोड़ने पर: 2x = 8 ⇒ x = 4, y = 2
संख्या = 42

समीकरण (1) और (3) से:
x + y = 6
y – x = 2
जोड़ने पर: 2y = 8 ⇒ y = 4, x = 2
संख्या = 24

✅ संख्याएं: 24 और 42 (कुल 2 संख्याएं)

📖 दो अंकों की संख्या वाले प्रश्न – बिल्कुल आसान भाषा में

⭐ मुख्य Formula:
अगर दो अंकों की संख्या में:
• दहाई का अंक = x
• इकाई का अंक = y

तो संख्या = 10x + y
और उलटी संख्या = 10y + x

💡 यह Formula क्यों?
मान लो संख्या है 42:
• दहाई का अंक (x) = 4
• इकाई का अंक (y) = 2
• संख्या = 4×10 + 2 = 40 + 2 = 42
• उलटी संख्या = 2×10 + 4 = 20 + 4 = 24

इस प्रश्न में Step-by-Step:
दिया है:
1. संख्या + उलटी संख्या = 66
2. अंकों का अंतर = 2

Step 1: मान लें
दहाई का अंक = x
इकाई का अंक = y
संख्या = 10x + y
उलटी संख्या = 10y + x

Step 2: पहली शर्त से समीकरण बनाएं
(10x + y) + (10y + x) = 66
11x + 11y = 66
x + y = 6 … (1)

Step 3: दूसरी शर्त से समीकरण
अंकों का अंतर = 2
इसका मतलब: x – y = 2 … (2)
या y – x = 2 … (3)
(दोनों cases संभव हैं)

Step 4: Case 1: समीकरण (1) और (2) को हल करें
x + y = 6
x – y = 2
────────── (जोड़ें)
2x = 8
x = 4
y = 6 – 4 = 2
संख्या = 10(4) + 2 = 42

Step 5: Case 2: समीकरण (1) और (3) को हल करें
x + y = 6
y – x = 2
────────── (जोड़ें)
2y = 8
y = 4
x = 6 – 4 = 2
संख्या = 10(2) + 4 = 24

उत्तर: 24 और 42 (कुल 2 संख्याएं)

परीक्षा में ध्यान दें:
1. हमेशा 10x + y लिखें (केवल x + y नहीं)
2. अंतर के दो cases चेक करें (x-y या y-x)
3. सभी संभव उत्तर लिखें
4. Verify करें: दोनों शर्तें check करें
• 42 + 24 = 66 ✓
• 4 – 2 = 2 ✓ (दोनों में)

💡 Common Mistakes से बचें:
❌ संख्या को सिर्फ x + y लिख दिया (10x + y होना चाहिए)
❌ सिर्फ एक case का उत्तर दिया (दोनों cases check करें)
❌ उलटी संख्या गलत लिखी (10x + y की जगह 10y + x)
❌ “कितनी संख्याएं हैं” भूल गए

याद रखने की Trick:
“दहाई दस गुणा, इकाई एक गुणा,
जोड़ो दोनों को, संख्या बन जाएगी”
10x + y = संख्या

ऐसे प्रश्नों के Common Types:
1. संख्या + उलटी = दिया हुआ
2. संख्या – उलटी = दिया हुआ
3. अंकों का योग = दिया हुआ
4. अंकों का अंतर = दिया हुआ
5. एक अंक दूसरे का दोगुना/तिगुना

सभी में Formula same: 10x + y

6. A.P. निर्धारित कीजिए जिसका तीसरा पद 5 और 7वां पद 9 है।

दिया है:
a₃ = 5 ⇒ a + 2d = 5 … (1)
a₇ = 9 ⇒ a + 6d = 9 … (2)

समीकरण (2) – (1):
4d = 4
d = 1

समीकरण (1) में रखने पर:
a + 2(1) = 5
a = 3

✅ A.P. = 3, 4, 5, 6, 7, 8, 9…

📖 AP निर्धारित करना जब दो पद दिए हों – बिल्कुल आसान भाषा में

⭐ मुख्य सूत्र याद रखें:
aₙ = a + (n-1)d
n वां पद = पहला पद + (n-1) × सार्वअंतर

इस तरह के प्रश्नों में Steps:
Step 1: दोनों पदों के लिए समीकरण बनाएं
Step 2: एक समीकरण से दूसरा घटाएं (d निकलेगा)
Step 3: d का मान पहले समीकरण में रखें (a निकलेगा)
Step 4: AP लिखें: a, a+d, a+2d, a+3d…

इस प्रश्न में:
a₃ = 5 → a + 2d = 5 … (1)
a₇ = 9 → a + 6d = 9 … (2)

(2) – (1):
4d = 4
d = 1

(1) में रखें:
a + 2(1) = 5
a = 3

AP: 3, 4, 5, 6, 7, 8, 9…

क्यों घटाते हैं?
जब घटाते हैं तो ‘a’ cancel हो जाता है:
(a + 6d) – (a + 2d) = 9 – 5
4d = 4
केवल d बचता है!

परीक्षा टिप:
• दोनों समीकरण बनाएं
• बड़े वाले से छोटा घटाएं
• Coefficients का अंतर = d के साथ गुणा
• d मिलने पर किसी भी एक में वापस रखें

7. आकृति में AB || PQ और AC || PR है। दर्शाइए कि BC || QR है।

थेल्स प्रमेय (BPT): यदि एक रेखा त्रिभुज की दो भुजाओं को समान अनुपात में काटे तो वह तीसरी भुजा के समांतर होती है

चरण 1: △POQ में देखें
दिया है: AB || PQ
थेल्स प्रमेय से:
OA/AP = OB/BQ … समीकरण (1)

चरण 2: △POR में देखें
दिया है: AC || PR
थेल्स प्रमेय से:
OA/AP = OC/CR … समीकरण (2)

चरण 3: दोनों समीकरण मिलाएं
समीकरण (1) और (2) से:
OA/AP = OB/BQ और OA/AP = OC/CR
इसलिए: OB/BQ = OC/CR

चरण 4: निष्कर्ष निकालें
△OQR में:
चूंकि OB/BQ = OC/CR
थेल्स प्रमेय के विलोम से:
BC || QR ✓

आसान भाषा में: जब दो रेखाएं किसी तीसरी रेखा के समांतर हों, तो उनको मिलाने वाली रेखा भी एक विशेष रेखा के समांतर होती है।

📖 थेल्स प्रमेय / आधारभूत समानुपातिकता प्रमेय (BPT) – बिल्कुल आसान भाषा में

⭐ थेल्स प्रमेय (Basic Proportionality Theorem):
अगर त्रिभुज की दो भुजाओं को एक रेखा काटे और वह तीसरी भुजा के समांतर हो, तो:
वह दोनों भुजाओं को समान अनुपात में काटती है

📐 सूत्र:
अगर DE || BC (त्रिभुज ABC में), तो:
AD/DB = AE/EC
या
AD/AB = AE/AC

💡 विलोम प्रमेय (Converse):
अगर एक रेखा त्रिभुज की दो भुजाओं को समान अनुपात में काटे, तो:
वह तीसरी भुजा के समांतर होती है

यानी: अगर AD/DB = AE/EC, तो DE || BC

इस प्रश्न में Step-by-Step:
दिया है: AB || PQ और AC || PR
सिद्ध करना है: BC || QR

Step 1: △POQ में देखें
AB || PQ है (दिया है)
BPT से: OA/AP = OB/BQ … (1)

Step 2: △POR में देखें
AC || PR है (दिया है)
BPT से: OA/AP = OC/CR … (2)

Step 3: समीकरण (1) और (2) को मिलाएं
OA/AP = OB/BQ … (1)
OA/AP = OC/CR … (2)

दोनों में OA/AP बराबर है, इसलिए:
OB/BQ = OC/CR

Step 4: BPT का विलोम लागू करें
△OQR में:
OB/BQ = OC/CR (Step 3 से)
BPT के विलोम से:
BC || QR (सिद्ध हुआ) ✓

परीक्षा में ध्यान दें:
1. पहचानें कौन सा triangle देखना है
2. Parallel lines को identify करें
3. BPT से ratio बनाएं
4. Common term को दोनों equations में खोजें
5. विलोम प्रमेय लगाना न भूलें (ratio से parallel prove करने के लिए)

💡 BPT कब लगाएं?
Direct BPT: जब parallel line दी हो → ratio निकालें
Converse BPT: जब ratio दिया हो → parallel prove करें

आम गलतियां जिनसे बचें:
❌ Ratio गलत लिखा (AD/DB की जगह AD/AB)
❌ त्रिभुज गलत चुना (confuse हो गए कि कौन सा triangle देखें)
❌ Converse apply करना भूल गए
❌ Common term को equate नहीं किया

याद रखने की Trick:
“Parallel है तो ratio same,
Ratio same तो parallel है ye game”

Parallel → Ratio (Direct)
Ratio → Parallel (Converse)

💡 BPT के Applications:
1. Parallel lines prove करने में
2. Triangle की भुजाओं के अनुपात निकालने में
3. Similar triangles में
4. आकृति में लंबाई निकालने में

8. निर्धारित करें कि क्या बिन्दु (1, 5), (2, 3) और (-2, -11) संरेखी हैं।

माना A(1, 5), B(2, 3), C(-2, -11)

AB की ढाल = (3 – 5)/(2 – 1) = -2/1 = -2

BC की ढाल = (-11 – 3)/(-2 – 2) = -14/-4 = 7/2

चूंकि AB की ढाल ≠ BC की ढाल

✅ अतः बिंदु संरेखी नहीं हैं।

📖 संरेखी बिंदु (Collinear Points) – बिल्कुल आसान भाषा में

संरेखी का मतलब:
तीन बिंदु जो एक ही सीधी रेखा पर हों
(Collinear = Co + Linear = एक साथ एक रेखा पर)

⭐ ढाल (Slope) का सूत्र:
दो बिंदुओं (x₁, y₁) और (x₂, y₂) के बीच:
m = (y₂ – y₁) / (x₂ – x₁)

संरेखी की शर्त:
तीन बिंदु A, B, C संरेखी होंगे यदि:
AB की ढाल = BC की ढाल = AC की ढाल
(सभी की slope same होनी चाहिए)

इस प्रश्न में:
A(1, 5), B(2, 3), C(-2, -11)

AB की ढाल = (3-5)/(2-1) = -2/1 = -2
BC की ढाल = (-11-3)/(-2-2) = -14/-4 = 7/2

-2 ≠ 7/2
इसलिए बिंदु संरेखी नहीं हैं

उदाहरण – संरेखी बिंदु:
A(0, 0), B(1, 2), C(2, 4)

AB की ढाल = (2-0)/(1-0) = 2
BC की ढाल = (4-2)/(2-1) = 2

दोनों same हैं → संरेखी हैं ✓

दूसरा तरीका – क्षेत्रफल सूत्र:
अगर तीन बिंदुओं से बने त्रिभुज का क्षेत्रफल = 0
तो बिंदु संरेखी हैं

Area = ½|x₁(y₂-y₃) + x₂(y₃-y₁) + x₃(y₁-y₂)|
यदि Area = 0 → संरेखी

परीक्षा टिप:
• ढाल विधि सबसे आसान है
• किन्हीं दो जोड़ों की ढाल निकालें
• Same हो → संरेखी, Different हो → नहीं
• ध्यान: denominator 0 न हो (vertical line)

9. △OPQ में, जिसका कोण P समकोण है, OP = 7 सेमी और OQ-PQ = 1 सेमी। sin Q और cos Q का मान ज्ञात करें।

दिया है: OP = 7 cm, OQ – PQ = 1
माना PQ = x, तो OQ = x + 1

पाइथागोरस प्रमेय से:
OP² + PQ² = OQ²
7² + x² = (x + 1)²
49 + x² = x² + 2x + 1
48 = 2x
x = 24

अतः PQ = 24 cm, OQ = 25 cm

sin Q = OP/OQ = 7/25
cos Q = PQ/OQ = 24/25

✅ sin Q = 7/25, cos Q = 24/25

📖 त्रिकोणमिति + पाइथागोरस प्रमेय – बिल्कुल आसान भाषा में

⭐ ऐसे प्रश्नों में दो चीजें लगती हैं:
1. पाइथागोरस प्रमेय – तीसरी भुजा निकालने के लिए
2. त्रिकोणमितीय अनुपात – sin, cos, tan निकालने के लिए

📐 पाइथागोरस प्रमेय:
समकोण त्रिभुज में:
(लंब)² + (आधार)² = (कर्ण)²
या
a² + b² = c²

📐 त्रिकोणमितीय अनुपात (किसी कोण θ के लिए):
sin θ = लंब/कर्ण (Perpendicular/Hypotenuse)
cos θ = आधार/कर्ण (Base/Hypotenuse)
tan θ = लंब/आधार (Perpendicular/Base)

इस प्रश्न में Step-by-Step:
दिया है:
• समकोण △OPQ (कोण P = 90°)
• OP = 7 cm
• OQ – PQ = 1

Step 1: अज्ञात को मान दें
माना PQ = x cm
तो OQ = x + 1 cm (क्योंकि OQ – PQ = 1)

Step 2: पाइथागोरस प्रमेय लगाएं
∠P = 90° पर समकोण है
तो OQ कर्ण है (सबसे लंबी भुजा)

OP² + PQ² = OQ²
7² + x² = (x + 1)²
49 + x² = x² + 2x + 1

Step 3: समीकरण हल करें
49 + x² = x² + 2x + 1
x² cancel हो जाएगा
49 = 2x + 1
48 = 2x
x = 24

Step 4: सभी भुजाओं का मान निकालें
PQ = x = 24 cm
OQ = x + 1 = 25 cm
OP = 7 cm (दिया हुआ)

Step 5: कोण Q के लिए अनुपात निकालें
कोण Q पर देखें:
• सामने की भुजा (लंब) = OP = 7
• बगल की भुजा (आधार) = PQ = 24
• कर्ण = OQ = 25

sin Q = लंब/कर्ण = OP/OQ = 7/25
cos Q = आधार/कर्ण = PQ/OQ = 24/25

💡 याद रखें – कोण के सामने वाली भुजा:
• कोण Q के सामने = OP (लंब)
• कोण Q के बगल में = PQ (आधार)
• समकोण के सामने = OQ (कर्ण – हमेशा सबसे लंबी)

परीक्षा टिप:
1. समकोण पहचानें – कर्ण के लिए
2. दिए हुए को x में लिखें (जैसे: OQ – PQ = 1)
3. पाइथागोरस से x निकालें
4. कोण के reference से लंब-आधार पहचानें
5. सही formula लगाएं (sin = लंब/कर्ण, cos = आधार/कर्ण)

आम गलतियां जिनसे बचें:
❌ (a+b)² को a² + b² लिखना (सही: a² + 2ab + b²)
❌ कर्ण को गलत पहचाना (समकोण के सामने हमेशा कर्ण)
❌ sin और cos में लंब-आधार उल्टा कर दिया
❌ कोण Q के लिए, कोण O की भुजाएं use कर दीं

याद रखने की Trick – SOH CAH TOA:
Sin = Opposite/Hypotenuse (सामने/कर्ण)
Cos = Adjacent/Hypotenuse (बगल/कर्ण)
Tan = Opposite/Adjacent (सामने/बगल)

💡 Famous Triplets (याद रखने लायक):
• 3, 4, 5 (और इसके गुणज: 6-8-10, 9-12-15)
• 5, 12, 13
• 7, 24, 25 ← यह प्रश्न में आया!
• 8, 15, 17
• 9, 40, 41

10. सिद्ध कीजिए: ∠PTQ = 2∠OPQ

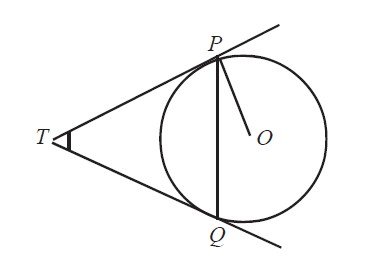
चित्र में: केंद्र O वाले वृत्त पर बाह्य बिंदु T से दो स्पर्श रेखाएं TP और TQ खींची गई हैं।

• बाह्य बिंदु से वृत्त पर खींची गई स्पर्श रेखाएं बराबर होती हैं
• त्रिज्या स्पर्श रेखा पर लंब होती है (90°)

चरण 1: मान लें
माना ∠PTQ = θ (जो हमें सिद्ध करना है)

चरण 2: △TPQ को समझें
TP = TQ (स्पर्श रेखाओं का गुण)
इसलिए △TPQ समद्विबाहु त्रिभुज है

चरण 3: आधार कोण निकालें
समद्विबाहु त्रिभुज में दोनों आधार कोण बराबर होते हैं:
∠TPQ = ∠TQP
त्रिभुज के कोणों का योग = 180°
∠PTQ + ∠TPQ + ∠TQP = 180°
θ + 2∠TPQ = 180°
∠TPQ = (180° – θ)/2 = 90° – θ/2

चरण 4: ∠OPT निकालें
त्रिज्या OP स्पर्श रेखा TP पर लंब है
इसलिए: ∠OPT = 90°

चरण 5: ∠OPQ निकालें
∠OPQ = ∠OPT – ∠TPQ
∠OPQ = 90° – (90° – θ/2)
∠OPQ = 90° – 90° + θ/2
∠OPQ = θ/2

चरण 6: अंतिम उत्तर
2 × ∠OPQ = 2 × θ/2 = θ
लेकिन θ = ∠PTQ
इसलिए: 2∠OPQ = ∠PTQ

✅ इति सिद्धम् (Hence Proved)

याद रखने का तरीका: बाहर का कोण अंदर के कोण का दोगुना होता है!

📖 वृत्त की स्पर्श रेखा और कोण सिद्ध करना – बिल्कुल आसान भाषा में

⭐ मुख्य गुणधर्म (जो हमेशा काम आते हैं):

1️⃣ बाह्य बिंदु से दोनों स्पर्श रेखाएं बराबर:
अगर बिंदु T से वृत्त पर TP और TQ स्पर्श रेखाएं हैं, तो:
TP = TQ

2️⃣ त्रिज्या स्पर्श रेखा पर लंबवत होती है:
स्पर्श बिंदु पर त्रिज्या और स्पर्श रेखा के बीच:
∠OPT = 90°

3️⃣ समद्विबाहु त्रिभुज का गुण:
अगर दो भुजाएं बराबर हों (TP = TQ), तो:
दोनों आधार कोण बराबर होते हैं

इस प्रश्न में Step-by-Step:
सिद्ध करना है: ∠PTQ = 2∠OPQ

Step 1: समद्विबाहु त्रिभुज पहचानें
TP = TQ (स्पर्श रेखाओं का गुण)
इसलिए △TPQ समद्विबाहु है
माना ∠PTQ = θ

Step 2: आधार कोण निकालें
△TPQ में कोणों का योग = 180°
∠PTQ + ∠TPQ + ∠TQP = 180°
θ + ∠TPQ + ∠TPQ = 180° (दोनों आधार कोण बराबर)
θ + 2∠TPQ = 180°
∠TPQ = (180° – θ)/2 = 90° – θ/2

Step 3: त्रिज्या की लंबवतता use करें
∠OPT = 90° (त्रिज्या ⊥ स्पर्श रेखा)

Step 4: ∠OPQ निकालें
देखें कि: ∠OPT = ∠OPQ + ∠TPQ
90° = ∠OPQ + (90° – θ/2)
∠OPQ = 90° – 90° + θ/2
∠OPQ = θ/2

Step 5: सिद्ध करें
2 × ∠OPQ = 2 × (θ/2) = θ
लेकिन θ = ∠PTQ
इसलिए: 2∠OPQ = ∠PTQ ✓

परीक्षा में ध्यान दें:
1. हमेशा छोटे-छोटे steps में लिखें
2. गुणधर्म का नाम बताएं (जैसे: “स्पर्श रेखाओं का गुण से…”)
3. Diagram में angles mark करें
4. मानना है तो clearly लिखें (माना ∠PTQ = θ)
5. “इति सिद्धम्” अंत में लिखें

💡 ऐसे प्रश्नों के Pattern:
• बाहर का कोण हमेशा अंदर के कोण का दोगुना होता है
• Key है: समद्विबाहु triangle + 90° angle

आम गलतियां जिनसे बचें:
❌ “TP = TQ क्यों?” नहीं बताया (गुणधर्म का नाम जरूरी)
❌ Angles को confuse कर दिया (∠OPQ और ∠TPQ अलग हैं)
❌ 90° angle को use नहीं किया
❌ Steps skip कर दिए (सीधे उत्तर लिख दिया)

याद रखने की Trick:
“स्पर्श बराबर, त्रिज्या लंब,
समद्विबाहु बनाओ, कोण निकलेगा संब”

TP = TQ → Isosceles
∠OPT = 90° → Use करो
बाहर = 2 × अंदर

💡 इस Topic के Common Theorems:
1. ∠PTQ = 2∠OPQ (यह प्रश्न)
2. ∠AOB = 180° – ∠APB (बाह्य बिंदु से)
3. ∠POQ + ∠PTQ = 180° (cyclic quadrilateral)

11. किसी कार के दो वाइपर हैं, परस्पर कभी आच्छादित नहीं होते हैं। प्रत्येक वाइपर की ब्लेड की लम्बाई 25 सेमी है और 115° के कोण तक घूमकर सफाई कर सकते हैं। प्रत्येक वाइपर के साथ जितना क्षेत्रफल साफ होता है, वह ज्ञात कीजिए।

दिया है: r = 25 cm, θ = 115°

त्रिज्यखंड का क्षेत्रफल = (θ/360°) × πr²
= (115°/360°) × (22/7) × 25 × 25
= (115/360) × (22/7) × 625

= (115 × 22 × 625) / (360 × 7)
= 1581250 / 2520
≈ 627.58 cm²

✅ प्रत्येक वाइपर द्वारा साफ किया गया क्षेत्रफल ≈ 628 cm²

📖 त्रिज्यखंड का व्यावहारिक उपयोग (Practical Applications) – बिल्कुल आसान भाषा में

⭐ Real Life में Sector Formula कहां Use होता है?
1. कार के वाइपर – यह प्रश्न! (Wiper blade जितना घूमता है, sector बनता है)
2. पंखे के ब्लेड – जितना area cover करता है
3. Sprinkler System – पानी कितने area में फैलता है
4. Pizza का टुकड़ा – एक slice का area
5. Clock की सुई – कितना area sweep करती है

📐 Sector का क्षेत्रफल (Formula Recap):
Area = (θ/360°) × πr²

जहां:
• θ = केंद्रीय कोण (degrees में)
• r = त्रिज्या (यहां = wiper blade की length)

इस Wiper वाले प्रश्न में:
समझें: Wiper blade एक केंद्र बिंदु से घूमती है
• Center point = वाइपर का base
• Blade length = radius = 25 cm
• जितने angle तक घूमती है = 115°
• जो area साफ होता है = Sector का area

Calculation:
Area = (115/360) × (22/7) × 25²
= (115/360) × (22/7) × 625
≈ 628 cm²

💡 ऐसे प्रश्नों में ध्यान दें:
1. Identify करें कि radius क्या है (वाइपर की length, पंखे का blade, etc.)
2. Angle कितना है (कितना घूमता है)
3. Formula सीधा लगाएं: (θ/360) × πr²
4. Units का ध्यान: cm में length → cm² में area

Common Variants:
• दोनों वाइपर मिलाकर? → 2 × एक वाइपर का area
• पंखे के 3 blades? → 3 × एक blade का area
• Sprinkler 360° घूमता है? → पूरा circle = πr²

याद रखें:
घूमने वाली चीज़ = Sector बनती है
Sector = Pizza slice shape = (θ/360) × πr²

Real life → Math:
घूमने की लंबाई = Radius (r)
कितना घूमी = Angle (θ)

12. निम्नलिखित सारणी 35 नगरों की साक्षरता दर (प्रतिशत में) दर्शाती है। माध्य साक्षरता दर ज्ञात कीजिए।

साक्षरता दर (%)	45—55	55—65	65—75	75—85	85—95
नगरों की संख्या	3	10	11	8	3

सारणी बनाना:

वर्ग	मध्य बिंदु (xᵢ)	बारंबारता (fᵢ)	fᵢxᵢ
45-55	50	3	150
55-65	60	10	600
65-75	70	11	770
75-85	80	8	640
85-95	90	3	270
कुल		Σfᵢ = 35	Σfᵢxᵢ = 2430

माध्य = Σfᵢxᵢ / Σfᵢ = 2430 / 35 = 69.43%

✅ माध्य साक्षरता दर = 69.43%

📖 वर्गीकृत आंकड़ों का माध्य (Mean of Grouped Data) – बिल्कुल आसान भाषा में

⭐ मुख्य सूत्र:
माध्य (x̄) = Σfᵢxᵢ / Σfᵢ
जहां:
• fᵢ = बारंबारता (frequency)
• xᵢ = वर्ग का मध्य बिंदु (class mark)
• Σ = योग (sum)

Step-by-Step विधि:
Step 1: प्रत्येक वर्ग का मध्य बिंदु निकालें
मध्य बिंदु (xᵢ) = (निचली सीमा + ऊपरी सीमा) / 2
जैसे: 45-55 का मध्य = (45+55)/2 = 50

Step 2: सारणी बनाएं (xᵢ, fᵢ, fᵢxᵢ)

Step 3: fᵢxᵢ निकालें (हर row में)
fᵢxᵢ = बारंबारता × मध्य बिंदु

Step 4: कुल योग निकालें
Σfᵢ = सभी frequencies का योग
Σfᵢxᵢ = सभी fᵢxᵢ का योग

Step 5: सूत्र में रखें
माध्य = Σfᵢxᵢ / Σfᵢ

इस प्रश्न में:
45-55: xᵢ=50, fᵢ=3, fᵢxᵢ=150
55-65: xᵢ=60, fᵢ=10, fᵢxᵢ=600
65-75: xᵢ=70, fᵢ=11, fᵢxᵢ=770
75-85: xᵢ=80, fᵢ=8, fᵢxᵢ=640
85-95: xᵢ=90, fᵢ=3, fᵢxᵢ=270

Σfᵢ = 35
Σfᵢxᵢ = 2430
माध्य = 2430/35 = 69.43%

क्यों मध्य बिंदु लेते हैं?
वर्ग में सभी मान नहीं दिए होते, केवल range दी होती है
इसलिए मान लेते हैं कि सभी मान वर्ग के बीच में हैं
यह एक approximate (अनुमानित) माध्य देता है

सामान्य गलतियां:
❌ मध्य बिंदु गलत निकालना
❌ fᵢxᵢ की जगह सिर्फ fᵢ जोड़ देना
❌ Σfᵢxᵢ और Σfᵢ का उलटा division करना
❌ Calculation में गड़बड़ी

परीक्षा टिप:
1. Table format में हल करें (साफ दिखता है)
2. सभी columns clearly label करें
3. फिर से check करें: Σfᵢ = कुल items
4. Units का ध्यान रखें (%, cm, etc.)
5. जांच: माध्य वर्गों की range में होना चाहिए

Alternative – Assumed Mean Method:
बड़ी संख्याओं में calculation आसान करने के लिए
x̄ = a + (Σfᵢdᵢ/Σfᵢ)
(जहां a = assumed mean, dᵢ = xᵢ – a)

13. 52 पत्तों की अच्छी फेंटी गई एक गड्डी में से एक पत्ता निकाला जाता है। निम्नलिखित को प्राप्त करने की प्रायिकता ज्ञात कीजिए:

(1) लाल रंग का बादशाह
लाल रंग के बादशाह = 2 (♥K, ♦K)
P = 2/52 = 1/26

(2) हुकुम का पत्ता
हुकुम के पत्ते = 13
P = 13/52 = 1/4

(3) लाल रंग की तस्वीर वाला पत्ता
लाल रंग के चित्र वाले पत्ते = 6 (♥J, ♥Q, ♥K, ♦J, ♦Q, ♦K)
P = 6/52 = 3/26

(4) एक तस्वीर वाला पत्ता
तस्वीर वाले पत्ते = 12 (4 Jack + 4 Queen + 4 King)
P = 12/52 = 3/13

✅ उत्तर: (1) 1/26, (2) 1/4, (3) 3/26, (4) 3/13

📖 प्रायिकता (Probability) – बिल्कुल आसान भाषा में

प्रायिकता का मतलब: किसी घटना के होने की संभावना (Chance)
सूत्र: P(घटना) = अनुकूल परिणाम / कुल संभव परिणाम

सिक्का उछालना:
कुल परिणाम = 2 (Head या Tail)
P(Head) = 1/2
P(Tail) = 1/2

पासा फेंकना (1 से 6):
कुल परिणाम = 6
P(सम संख्या) = 3/6 = 1/2 (2, 4, 6)
P(5 आना) = 1/6

ताश की गड्डी (52 पत्ते):
• 4 प्रकार: ♠ (हुकुम), ♥ (पान), ♦ (ईंट), ♣ (चिड़ी)
• हर प्रकार में 13 पत्ते (A, 2-10, J, Q, K)
• लाल रंग: ♥ और ♦ (कुल 26)
• काला रंग: ♠ और ♣ (कुल 26)
• तस्वीर वाले: J, Q, K (कुल 12)

आसान सवाल:
Q: एक पत्ता निकालें – King मिलने की प्रायिकता?
हल:
• King कितने हैं? = 4 (हर प्रकार में 1)
• कुल पत्ते = 52
• P(King) = 4/52 = 1/13

मुख्य बातें:
• प्रायिकता हमेशा 0 और 1 के बीच होती है
• P = 0 = असंभव घटना
• P = 1 = निश्चित घटना
• P(घटना) + P(घटना नहीं) = 1

परीक्षा टिप:
1. पहले गिनें – “कितने अनुकूल हैं?”
2. फिर गिनें – “कुल कितने हैं?”
3. भाग दें: अनुकूल / कुल
4. सरल करें (जैसे 4/52 = 1/13)

खण्ड-स (SECTION-C)

दीर्घ उत्तरीय प्रश्न (Long Answer Type Questions) – प्रत्येक 3 अंक

14. दो क्रमागत धनात्मक पूर्णांक ज्ञात कीजिए जिनके वर्गों का योग 365 हो।

प्रश्न का अर्थ: दो लगातार संख्याएं (जैसे 5 और 6) ढूंढनी हैं जिनके वर्ग जोड़ने पर 365 आए

चरण 1: माना
पहली संख्या = x
दूसरी संख्या = x + 1 (क्योंकि लगातार है)
उदाहरण: अगर पहली 5 है तो दूसरी 6

चरण 2: समीकरण बनाएं
प्रश्न के अनुसार: पहली का वर्ग + दूसरी का वर्ग = 365
x² + (x+1)² = 365

चरण 3: (x+1)² को खोलें
याद रखें: (a+b)² = a² + 2ab + b²
(x+1)² = x² + 2x + 1

अब समीकरण में रखें:
x² + x² + 2x + 1 = 365
2x² + 2x + 1 = 365
2x² + 2x = 364
2x² + 2x – 364 = 0

चरण 4: 2 से भाग दें (सरल बनाने के लिए)
x² + x – 182 = 0

चरण 5: गुणनखंड बनाएं
हमें दो ऐसी संख्याएं चाहिए जिनका:
• गुणनफल = -182
• योग = 1
वे संख्याएं हैं: +14 और -13
(क्योंकि 14 × (-13) = -182 और 14 + (-13) = 1)

x² + 14x – 13x – 182 = 0
x(x + 14) – 13(x + 14) = 0
(x + 14)(x – 13) = 0

चरण 6: x का मान निकालें
x + 14 = 0 या x – 13 = 0
x = -14 या x = 13

चूंकि संख्या धनात्मक चाहिए (Positive)
इसलिए x = 13 ✓

✅ उत्तर: पहली संख्या = 13, दूसरी संख्या = 14

चरण 7: जांच करें (बहुत ज़रूरी!)
13² + 14² = ?
= 169 + 196
= 365 ✓ (सही है!)

लगातार संख्याएं = x और (x+1)
जैसे: 5 और 6, या 10 और 11, या 13 और 14

📖 क्रमागत संख्याओं वाले प्रश्न – बिल्कुल आसान भाषा में

⭐ क्रमागत संख्याएं क्या हैं?
वे संख्याएं जो एक के बाद एक आती हैं
• लगातार संख्याएं: x, x+1, x+2 (जैसे: 5, 6, 7)
• लगातार सम संख्याएं: x, x+2, x+4 (जैसे: 4, 6, 8)
• लगातार विषम संख्याएं: x, x+2, x+4 (जैसे: 3, 5, 7)

इस प्रश्न का Pattern:
“दो क्रमागत संख्याओं के वर्गों का योग = 365”

Step 1: सही notation चुनें
पहली संख्या = x
दूसरी संख्या = x + 1 (अगली संख्या)

Step 2: समीकरण setup करें
x² + (x+1)² = 365

Step 3: (x+1)² को expand करें
(x+1)² = x² + 2x + 1
इसलिए: x² + x² + 2x + 1 = 365
2x² + 2x + 1 = 365

Step 4: मानक रूप में लाएं
2x² + 2x – 364 = 0
दोनों पक्षों को 2 से भाग दें:
x² + x – 182 = 0

Step 5: हल करें (गुणनखंड या सूत्र से)
(x + 14)(x – 13) = 0
x = -14 या x = 13
धनात्मक चाहिए, इसलिए x = 13

Step 6: MUST verify करें!
13² + 14² = 169 + 196 = 365 ✓

परीक्षा टिप:
1. Notation decide करें: क्रमागत = x, x+1
2. (x+1)² सही expand करें (common mistake!)
3. Simplify करें (divide by common factor)
4. Negative value reject करें (अगर positive मांगा हो)
5. हमेशा verify करें – marks के लिए ज़रूरी!

💡 Common Patterns:
• वर्गों का योग: x² + (x+1)² = given
• वर्गों का अंतर: (x+1)² – x² = given
• गुणनफल: x(x+1) = given
• तीन क्रमागत: x, x+1, x+2

आम गलतियां जिनसे बचें:
❌ (x+1)² को x² + 1 लिखना (सही: x² + 2x + 1)
❌ Verification skip करना
❌ Negative answer लिख दिया जब positive मांगा था
❌ Simplification नहीं की (2x² + 2x = 0 को x² + x = 0 नहीं बनाया)

याद रखने की Trick:
“एक्स है पहला, एक्स+वन दूजा,
वर्ग करो expand करो, जोड़ो बराबर पूजा”

x और (x+1) → Consecutive
हमेशा verify करना!

अथवा / OR

14 (OR). द्विघात समीकरण kx(x-2) + 6 = 0 के मूल बराबर हों तो k का मान ज्ञात कीजिए।

समीकरण: kx(x-2) + 6 = 0
kx² – 2kx + 6 = 0

यहाँ a = k, b = -2k, c = 6

मूल बराबर होने की शर्त: b² – 4ac = 0
(-2k)² – 4(k)(6) = 0
4k² – 24k = 0
4k(k – 6) = 0

k = 0 या k = 6
k ≠ 0 (क्योंकि यह द्विघात समीकरण है)

✅ अतः k = 6

15. अनुपात ज्ञात कीजिए जिसमें रेखाखण्ड को जोड़ने वाली रेखा A(1, -5) और B(-4, 5) को x-अक्ष विभाजित करती है। इस विभाजन बिन्दु के निर्देशांक भी ज्ञात कीजिए।

माना x-अक्ष पर बिंदु P(x, 0) है जो AB को m:n में विभाजित करता है।

विभाजन सूत्र से y-निर्देशांक:
0 = (m × 5 + n × (-5)) / (m + n)
0 = (5m – 5n) / (m + n)
5m – 5n = 0
m = n
अतः अनुपात m:n = 1:1

x-निर्देशांक:
x = (1 × (-4) + 1 × 1) / (1 + 1)
x = (-4 + 1) / 2
x = -3/2

✅ अनुपात = 1:1, विभाजन बिंदु = (-3/2, 0)

अथवा / OR

15 (OR). यदि A और B क्रमशः (-2, -2) और (2, -4) हो तो बिन्दु P के निर्देशांक ज्ञात कीजिए ताकि AP = 3/7 AB हो और P रेखाखण्ड AB पर स्थित हो।

दिया है: AP = 3/7 AB
अतः AP:PB = 3:4

विभाजन सूत्र से:
x = (3 × 2 + 4 × (-2)) / (3 + 4) = (6 – 8) / 7 = -2/7
y = (3 × (-4) + 4 × (-2)) / (3 + 4) = (-12 – 8) / 7 = -20/7

✅ P = (-2/7, -20/7)

📖 विभाजन सूत्र / Section Formula – बिल्कुल आसान भाषा में

⭐ विभाजन सूत्र क्या है?
जब कोई बिंदु P, दो बिंदुओं A और B को जोड़ने वाली रेखा को किसी अनुपात में विभाजित करता है, तो P के निर्देशांक निकालने का formula

📐 Section Formula (Internal Division):
अगर बिंदु P, बिंदु A(x₁, y₁) और B(x₂, y₂) को m:n में विभाजित करता है, तो:

P(x, y) = ((mx₂ + nx₁)/(m+n), (my₂ + ny₁)/(m+n))

💡 याद रखने का तरीका – “Cross Multiply”:
• x-निर्देशांक: m का weight x₂ पर, n का weight x₁ पर
• y-निर्देशांक: m का weight y₂ पर, n का weight y₁ पर
• फिर दोनों को (m+n) से divide करो

Q15 का पहला भाग – Step-by-Step:
A(1, -5), B(-4, 5), x-अक्ष पर विभाजन बिंदु

Step 1: समझें कि x-axis पर y = 0
विभाजन बिंदु P(x, 0) है

Step 2: y-निर्देशांक वाला formula use करें
0 = (m × 5 + n × (-5))/(m+n)
0 = (5m – 5n)/(m+n)
5m – 5n = 0
m = n → अनुपात = 1:1

Step 3: x-निर्देशांक निकालें
x = (1×(-4) + 1×1)/(1+1)
x = (-4+1)/2 = -3/2

Q15 का दूसरा भाग (OR) – Step-by-Step:
A(-2, -2), B(2, -4), AP = 3/7 AB

Step 1: Ratio निकालें
अगर AP = 3/7 AB
तो PB = AB – AP = 7/7 – 3/7 = 4/7 AB
AP:PB = 3:4

Step 2: Section Formula लगाएं (m=3, n=4)
x = (3×2 + 4×(-2))/(3+4) = (6-8)/7 = -2/7
y = (3×(-4) + 4×(-2))/(3+4) = (-12-8)/7 = -20/7

💡 Special Cases (Important!):

1️⃣ Mid-Point (बिंदु ठीक बीच में):
अगर P, AB का mid-point है (1:1)
P = ((x₁+x₂)/2, (y₁+y₂)/2)

2️⃣ x-axis पर विभाजन:
y = 0 रखो, m:n निकालो

3️⃣ y-axis पर विभाजन:
x = 0 रखो, m:n निकालो

परीक्षा में ध्यान दें:
1. Ratio पहचानें: AP:PB or m:n क्या है
2. Points identify करें: कौन सा A और कौन सा B है
3. Formula सही लगाएं: mx₂+nx₁ (NOT mx₁+nx₂)
4. (m+n) से divide: भूलें नहीं!
5. Signs का ध्यान: Negative coordinates में

आम गलतियां जिनसे बचें:
❌ m और n को उल्टा लगा दिया (mx₁+nx₂ की जगह mx₂+nx₁)
❌ AP = 3/7 AB को सीधा 3:7 मान लिया (सही: 3:4)
❌ (m+n) से divide करना भूल गए
❌ Negative signs में गड़बड़ी
❌ Mid-point formula को section formula से confuse कर दिया

याद रखने की Trick:
“Cross करो ratio को coordinates से,
म से दो, न से एक, जोड़ो बांटो sum से”

m से B के coordinates, n से A के coordinates
फिर (m+n) से divide

💡 Applications:
1. रेखा को किसी अनुपात में विभाजित करना
2. Mid-point निकालना
3. Trisection points (3 बराबर भागों में)
4. x-axis या y-axis पर intersection point

16. सिद्ध कीजिए:
(cot A – cos A) / (cot A + cos A) = (cosec A – 1) / (cosec A + 1)

बायां पक्ष (LHS):
= (cot A – cos A) / (cot A + cos A)
= (cos A/sin A – cos A) / (cos A/sin A + cos A)
= [cos A(1 – sin A) / sin A] / [cos A(1 + sin A) / sin A]
= (1 – sin A) / (1 + sin A)

अंश और हर में (1 – sin A) से गुणा करने पर:
= [(1 – sin A)²] / [(1 + sin A)(1 – sin A)]
= (1 – sin A)² / (1 – sin²A)
= (1 – sin A)² / cos²A

दायां पक्ष (RHS):
= (cosec A – 1) / (cosec A + 1)
= (1/sin A – 1) / (1/sin A + 1)
= (1 – sin A) / (1 + sin A)

✅ LHS = RHS (इति सिद्धम्)

अथवा / OR

16 (OR). सिद्ध कीजिए:
√[(1 + sin A) / (1 – sin A)] = sec A + tan A
जहाँ A न्यून कोण है।

बायां पक्ष:
= √[(1 + sin A) / (1 – sin A)]

अंश और हर में (1 + sin A) से गुणा:
= √[(1 + sin A)² / (1 – sin²A)]
= √[(1 + sin A)² / cos²A]
= (1 + sin A) / cos A
= 1/cos A + sin A/cos A
= sec A + tan A

✅ = RHS (इति सिद्धम्)

📖 त्रिकोणमितीय सर्वसमिकाएं सिद्ध करना – बिल्कुल आसान भाषा में

⭐ मुख्य त्रिकोणमितीय सर्वसमिकाएं (याद रखें!):

1️⃣ Pythagorean Identities:
• sin²θ + cos²θ = 1
• 1 + tan²θ = sec²θ
• 1 + cot²θ = cosec²θ

2️⃣ Reciprocal Relations:
• cosec θ = 1/sin θ
• sec θ = 1/cos θ
• cot θ = 1/tan θ

3️⃣ Quotient Relations:
• tan θ = sin θ/cos θ
• cot θ = cos θ/sin θ

💡 सिद्ध करने के Steps:
1. एक पक्ष चुनें (आमतौर पर जटिल वाला – LHS)
2. सर्वसमिकाएं लगाएं (ऊपर वाली)
3. Simplify करें (जोड़ो, घटाओ, cancel करो)
4. दूसरे पक्ष तक पहुंचें (RHS)
5. लिखें “इति सिद्धम्”

Q16 पहला भाग – Step-by-Step:
सिद्ध करें: (cot A – cos A)/(cot A + cos A) = (cosec A – 1)/(cosec A + 1)

LHS से शुरू करें:
= (cot A – cos A)/(cot A + cos A)

cot A = cos A/sin A लगाएं:
= (cos A/sin A – cos A)/(cos A/sin A + cos A)
= [cos A(1/sin A – 1)]/[cos A(1/sin A + 1)]
cos A cancel हो जाएगा:
= (1 – sin A)/(1 + sin A)

RHS को भी simplify करें:
= (cosec A – 1)/(cosec A + 1)
= (1/sin A – 1)/(1/sin A + 1)
= (1 – sin A)/(1 + sin A)

LHS = RHS ✓ इति सिद्धम्

Q16 दूसरा भाग (OR) – Step-by-Step:
सिद्ध करें: √[(1 + sin A)/(1 – sin A)] = sec A + tan A

Rationalize करें:
अंश-हर में (1 + sin A) से गुणा:
= √[(1 + sin A)²/(1 – sin²A)]

Identity लगाएं: 1 – sin²A = cos²A
= √[(1 + sin A)²/cos²A]
= (1 + sin A)/cos A

अलग-अलग करें:
= 1/cos A + sin A/cos A
= sec A + tan A ✓

💡 Common Techniques:

1️⃣ Everything को sin और cos में बदलो:
tan, cot, sec, cosec सब को sin/cos में लिखो

2️⃣ Rationalization:
(a-b) दिखे तो (a+b) से गुणा करो → a²-b² बनेगा

3️⃣ Common Factor निकालो:
जैसे: cos A(1-sin A) में से cos A बाहर

4️⃣ 1 को Replace करो:
• 1 = sin²θ + cos²θ
• 1 = sec²θ – tan²θ

परीक्षा में ध्यान दें:
1. सिर्फ एक पक्ष को simplify करें (usually LHS)
2. Identities सही लगाएं (याद रखें!)
3. Steps clearly लिखें – हर step में marks
4. Cancel होने वाले terms highlight करें
5. “इति सिद्धम्” अंत में जरूर लिखें

आम गलतियां जिनसे बचें:
❌ दोनों पक्षों को एक साथ simplify किया (only one side!)
❌ Identities गलत लगाईं (1+tan²θ = sec²θ को 1+cot²θ लिख दिया)
❌ Rationalization में sign mistake (a²-b² भूल गए)
❌ Steps skip किए (direct answer लिख दिया)
❌ LHS ≠ RHS आ गया लेकिन mistake ढूंढी नहीं

याद रखने की Trick – “SSC टेक”:
Simplify one side only
Substitute identities
Cancel common terms

Main 3 Identities हमेशा याद रखें:
sin² + cos² = 1
1 + tan² = sec²
1 + cot² = cosec²

💡 Quick Identity Tricks:
• 1 – sin²A देखें? → cos²A लिखो
• 1 – cos²A देखें? → sin²A लिखो
• sec²A – 1 देखें? → tan²A लिखो
• cosec²A – 1 देखें? → cot²A लिखो
• (a+b)(a-b) देखें? → a² – b² करो

17. निम्न सारणी किसी स्कूल की कक्षा X की 51 लड़कियों की ऊँचाइयों (सेमी में) का बंटन दर्शात है:

ऊँचाई (cm में)	140 से कम	145 से कम	150 से कम	155 से कम	160 से कम	165 से कम
लड़कियों की संख्या	4	11	29	40	46	51

माध्यक ऊँचाई ज्ञात कीजिए।

माध्यक क्या है? बीच वाली संख्या – आधी संख्याएं इससे छोटी, आधी इससे बड़ी

चरण 1: पहले सारणी को समझें
“140 से कम” का मतलब: 0 से 140 तक की ऊंचाई
“145 से कम” का मतलब: 0 से 145 तक की ऊंचाई
इसी तरह आगे…

चरण 2: वर्ग अंतराल और बारंबारता बनाएं

ऊंचाई (cm)	लड़कियां (f)	कुल लड़कियां अब तक (cf)	कैसे निकाला
0-140	4	4	दिया है
140-145	7	11	11 – 4 = 7
145-150	18	29	29 – 11 = 18 (माध्यक वर्ग)
150-155	11	40	40 – 29 = 11
155-160	6	46	46 – 40 = 6
160-165	5	51	51 – 46 = 5
कुल लड़कियां (N)		51

चरण 3: माध्यक वर्ग ढूंढें
N/2 = 51/2 = 25.5

अब देखें कि 25.5 कहाँ है:
• 11 तक – नहीं (छोटा है)
• 29 तक – हाँ! यहीं है ✓

इसलिए माध्यक वर्ग = 145-150

माध्यक सूत्र: Median = l + [(N/2 – cf)/f] × h

चरण 4: सूत्र की चीजें पहचानें
• l (Lower limit) = 145 (माध्यक वर्ग की निचली सीमा)
• N/2 = 25.5 (आधी लड़कियां)
• cf = 11 (पिछले वर्ग तक की कुल लड़कियां)
• f = 18 (माध्यक वर्ग में लड़कियां)
• h = 5 (वर्ग का size: 150-145 = 5)

चरण 5: सूत्र में मान डालें
Median = 145 + [(25.5 – 11) / 18] × 5
= 145 + [14.5 / 18] × 5
= 145 + 0.806 × 5
= 145 + 4.03
= 149.03 cm

✅ माध्यक ऊँचाई = 149.03 cm (लगभग 149 cm)

मतलब: आधी लड़कियां (25.5) 149 cm से छोटी हैं, और आधी इससे लंबी हैं

📖 माध्यक (Median) – Grouped Data – बिल्कुल आसान भाषा में

⭐ माध्यक क्या है?
बीच वाली संख्या – आधे लोग इससे छोटे, आधे इससे बड़े
उदाहरण: 1, 2, 3, 4, 5 → माध्यक = 3 (बीच में है)

📐 Grouped Data के लिए माध्यक सूत्र:
Median = l + [(N/2 – cf)/f] × h

जहां:
• l = Lower boundary (माध्यक वर्ग की निचली सीमा)
• N = कुल frequency (Total items)
• cf = Cumulative frequency (माध्यक वर्ग से पहले तक की कुल frequency)
• f = माध्यक वर्ग की frequency
• h = Class size (वर्ग का आकार)

💡 “से कम” (Less than) Type Data को कैसे Handle करें?
यह Q17 में है – “140 से कम”, “145 से कम” etc.

Step 1: Cumulative frequency पहले से दी हुई है!
“145 से कम” = 11 का मतलब: 11 लड़कियां 145 cm से कम हैं

Step 2: Actual frequency निकालो (Subtraction से):
140-145: 11 – 4 = 7 लड़कियां
145-150: 29 – 11 = 18 लड़कियां

Step 3: Table बनाओ और median निकालो

माध्यक वर्ग कैसे ढूंढें? (सबसे Important!)

Step 1: N/2 निकालें
N = 51 (total items)
N/2 = 51/2 = 25.5

Step 2: Cumulative frequency (cf) में देखें
कहां पर cf, N/2 से पहली बार बड़ा या बराबर हो रहा है?

• cf = 4 (छोटा है 25.5 से) ✗
• cf = 11 (छोटा है 25.5 से) ✗
• cf = 29 (बड़ा है 25.5 से) ✓ ← यहीं है!

इसलिए माध्यक वर्ग = 145-150

इस प्रश्न में पूरा Calculation:

माध्यक वर्ग = 145-150
• l = 145
• N/2 = 25.5
• cf = 11 (145 से पहले तक)
• f = 18 (145-150 वर्ग में)
• h = 5 (150-145)

Median = 145 + [(25.5-11)/18] × 5
= 145 + [14.5/18] × 5
= 145 + 4.03
= 149.03 cm

💡 Quick Tips:
1. N/2 सबसे important है – यही बताता है median कहां है
2. cf table जरूर बनाएं – बिना इसके confusion होगा
3. “से कम” में cf पहले से मिली है – बस frequency निकालो
4. h हमेशा positive – upper limit – lower limit
5. Formula में सही values रखो – l, cf, f confuse न हों

परीक्षा में ध्यान दें:
1. Table format में हल करें – साफ दिखता है
2. N/2 पहले निकालें और highlight करें
3. Median class clearly बताएं
4. Formula लिखें – फिर values डालें
5. Units याद रखें (cm, kg, etc.)

आम गलतियां जिनसे बचें:
❌ Median class गलत चुना (N/2 देखना भूल गए)
❌ cf में गड़बड़ी (subtraction गलत किया)
❌ l की जगह upper limit लिख दिया
❌ Formula में cf और f confuse हो गए
❌ h negative आ गया (145-150 की जगह 150-145)

याद रखने की Trick:
“एन बटा दो जहाँ आए,
वो वर्ग median कहलाए”

Median = l + [(N/2 – cf)/f] × h

l से शुरू, cf घटा, f से बांट, h से गुणा!

💡 माध्य, माध्यक, बहुलक में अंतर:
• माध्य (Mean) = Average = सब जोड़ो और divide करो
• माध्यक (Median) = Middle value = बीच वाली
• बहुलक (Mode) = Most frequent = सबसे ज्यादा बार आने वाली

अथवा / OR

17 (OR). यदि नीचे दिए हुए बंटन का माध्यक 28.5 हो तो x और y के मान ज्ञात कीजिए:

वर्ग अंतराल	0-10	10-20	20-30	30-40	40-50	50-60	कुल
बारंबारता	5	x	20	15	y	5	60

चरण 1: बारंबारताओं का योग:
5 + x + 20 + 15 + y + 5 = 60
x + y + 45 = 60
x + y = 15 … (1)

चरण 2: संचयी बारंबारता सारणी:
0-10: cf = 5
10-20: cf = 5 + x
20-30: cf = 25 + x (माध्यक वर्ग)
30-40: cf = 40 + x
40-50: cf = 40 + x + y
50-60: cf = 60

चरण 3: माध्यक सूत्र:
28.5 = 20 + [(30 – (5 + x)) / 20] × 10
8.5 = [(25 – x) / 20] × 10
8.5 = (25 – x) / 2
17 = 25 – x
x = 8

समीकरण (1) से:
8 + y = 15
y = 7

✅ x = 8, y = 7

खण्ड-द (SECTION-D)

निबंधात्मक प्रश्न (Essay Type Questions) – प्रत्येक 4 अंक

18. भूमि के एक बिन्दु P से 10 मीटर ऊँचे भवन के शिखर का उन्नयन कोण 30° है। भवन पर एक ध्वज लगा है। P से ध्वज के शिखर का उन्नयन कोण 45° है। ध्वजदंड की लम्बाई ज्ञात करें। (√3 = 1.73)

माना:
• भवन की ऊंचाई = AB = 10 m
• ध्वजदंड की लंबाई = BC = h m
• भूमि पर बिंदु P से दूरी = PB = x m

छोटे त्रिभुज PAB में:
tan 30° = AB/PB
1/√3 = 10/x
x = 10√3 m
x = 10 × 1.73 = 17.3 m

बड़े त्रिभुज PAC में (पूरी ऊंचाई):
tan 45° = AC/PB = (AB + BC)/x
1 = (10 + h) / 10√3
10√3 = 10 + h
h = 10√3 – 10
h = 10(√3 – 1)
h = 10(1.73 – 1)
h = 10 × 0.73
h = 7.3 m

✅ ध्वजदंड की लंबाई = 7.3 मीटर

📖 ऊंचाई और दूरी (Heights & Distances) – बिल्कुल आसान भाषा में

⭐ मुख्य शब्दावली:

1️⃣ उन्नयन कोण (Angle of Elevation):
जब आप नीचे से ऊपर देखते हैं (जैसे: मीनार को देखना)
क्षैतिज रेखा और दृष्टि रेखा के बीच का कोण

2️⃣ अवनमन कोण (Angle of Depression):
जब आप ऊपर से नीचे देखते हैं (जैसे: मीनार से जमीन देखना)
क्षैतिज रेखा और दृष्टि रेखा के बीच का कोण

📐 मुख्य सूत्र:
tan θ = लंब/आधार = ऊंचाई/दूरी

याद रखें:
• tan 30° = 1/√3 ≈ 0.577
• tan 45° = 1
• tan 60° = √3 ≈ 1.732

• sin 30° = 1/2, cos 30° = √3/2
• sin 45° = 1/√2, cos 45° = 1/√2
• sin 60° = √3/2, cos 60° = 1/2

इस प्रश्न में Step-by-Step:
दिया है:
• भवन की ऊंचाई (AB) = 10 m
• भवन के शिखर का उन्नयन कोण = 30°
• ध्वज के शिखर का उन्नयन कोण = 45°

Step 1: आरेख बनाएं और मान दें
माना:
• ध्वजदंड की लंबाई = h m
• P से भवन की दूरी = x m

Step 2: पहले triangle में tan लगाएं (30°)
△PAB में (भवन तक):
tan 30° = AB/PB
1/√3 = 10/x
x = 10√3 m

Step 3: दूसरे triangle में tan लगाएं (45°)
△PAC में (पूरी ऊंचाई तक):
tan 45° = AC/PB
1 = (10 + h)/10√3
10√3 = 10 + h

Step 4: h निकालें
h = 10√3 – 10
h = 10(√3 – 1)
h = 10(1.73 – 1)
h = 10 × 0.73
h = 7.3 m

परीक्षा में ध्यान दें:
1. साफ आरेख बनाएं – सभी points, heights, distances mark करें
2. समकोण त्रिभुज identify करें
3. कौन सा ratio use करें decide करें (tan सबसे common)
4. दिए गए मान accurately use करें (√3 = 1.73)
5. इकाई याद रखें (m, cm, etc.)

💡 Heights & Distances के Common Patterns:
Pattern 1: एक object, एक angle → सीधा tan लगाओ
Pattern 2: दो angles, दो heights → दो equations बनाओ
Pattern 3: एक ही object के दो angles → distance निकालो

आम गलतियां जिनसे बचें:
❌ tan के बजाय sin/cos लगा दिया (बिना reason)
❌ ऊंचाई और दूरी को उल्टा कर दिया (tan = ऊंचाई/दूरी)
❌ √3 का मान गलत लिया या नहीं लिया
❌ दो triangles को confuse कर दिया
❌ आरेख नहीं बनाया (marks कट सकते हैं!)

याद रखने की Trick:
“टैन है बेस्ट ऊंचाई दूरी के लिए,
ऊपर लिखो ऊंचाई, नीचे दूरी के लिए”

tan θ = Height/Distance

आरेख जरूर बनाओ → marks मिलते हैं!

💡 Common Values (याद रखें!):

Angle	sin	cos	tan
30°	1/2	√3/2	1/√3
45°	1/√2	1/√2	1
60°	√3/2	1/2	√3

अथवा / OR

18 (OR). समुद्रतल से 75 m ऊंचे लाइटहाउस से दो जहाजों के अवनमन कोण 30° और 45° हैं। यदि लाइटहाउस की एक ही ओर एक जहाज ठीक दूसरे जहाज के पीछे हो तो जहाजों के बीच की दूरी ज्ञात करें।

माना:
• लाइटहाउस की ऊंचाई = AB = 75 m
• पहले जहाज की दूरी = BC = y m (45° वाला)
• दूसरे जहाज की दूरी = BD = x m (30° वाला)

पहले जहाज के लिए (45°):
tan 45° = AB/BC
1 = 75/y
y = 75 m

दूसरे जहाज के लिए (30°):
tan 30° = AB/BD
1/√3 = 75/x
x = 75√3
x = 75 × 1.732
x = 129.9 m

जहाजों के बीच की दूरी:
= x – y
= 129.9 – 75
= 54.9 m

✅ जहाजों के बीच की दूरी ≈ 54.9 मीटर

19. एक खिलौना एक अर्धगोले पर रखा एक शंकु के आकार का है। शंकु की ऊँचाई 2 cm है और आधार का व्यास 4 cm है। खिलौने का आयतन ज्ञात कीजिए। यदि एक समकक्ष बेलन उसी सामान्य आधार वाला हो तो बेलन और खिलौने के आयतनों में अंतर भी ज्ञात कीजिए। (π = 3.14)

दिया है:
• शंकु की ऊंचाई (h) = 2 cm
• आधार का व्यास (d) = 4 cm
• त्रिज्या (r) = 2 cm

खिलौने का आयतन:
= शंकु का आयतन + अर्धगोले का आयतन
= (1/3)πr²h + (2/3)πr³
= (1/3)πr²(h + 2r)
= (1/3) × 3.14 × 2² × (2 + 2×2)
= (1/3) × 3.14 × 4 × 6
= (3.14 × 24) / 3
= 75.36 / 3
= 25.12 cm³

बेलन का आयतन:
बेलन की ऊंचाई = शंकु की ऊंचाई + अर्धगोले की त्रिज्या
H = 2 + 2 = 4 cm
आयतन = πr²H
= 3.14 × 2² × 4
= 3.14 × 4 × 4
= 50.24 cm³

अंतर:
= 50.24 – 25.12
= 25.12 cm³

✅ खिलौने का आयतन = 25.12 cm³
आयतनों में अंतर = 25.12 cm³

अथवा / OR

19 (OR). एक गुलाबजामुन में उसके आयतन की लगभग 30% चीनी की चाशनी होती है। 45 गुलाबजामुन में कितनी लगभग चाशनी होगी, यदि प्रत्येक गुलाबजामुन एक बेलन के आकार का है, जिसके दोनों सिरे अर्धगोलाकार हैं तथा इसकी लम्बाई 5 सेमी और व्यास 2.8 सेमी है।

दिया है:
• लंबाई (l) = 5 cm
• व्यास (d) = 2.8 cm
• त्रिज्या (r) = 1.4 cm
• बेलनाकार भाग की लंबाई = 5 – 2r = 5 – 2.8 = 2.2 cm

एक गुलाबजामुन का आयतन:
= बेलन का आयतन + 2 अर्धगोलों का आयतन
= πr²h + 2 × (2/3)πr³
= πr²h + (4/3)πr³
= πr²[h + (4r/3)]
= (22/7) × 1.4² × [2.2 + (4×1.4)/3]
= (22/7) × 1.96 × [2.2 + 1.867]
= (22/7) × 1.96 × 4.067
≈ 25.05 cm³

चाशनी प्रति गुलाबजामुन:
= 30% × 25.05
= 0.30 × 25.05
= 7.515 cm³

45 गुलाबजामुन में चाशनी:
= 45 × 7.515
= 338.175 cm³
≈ 338 cm³

✅ 45 गुलाबजामुन में लगभग 338 cm³ चाशनी होगी।

📖 संयुक्त ठोस आकृतियों का आयतन – बिल्कुल आसान भाषा में

⭐ संयुक्त ठोस (Combined Solids) क्या हैं?
जब दो या अधिक ठोस shapes को मिला दिया जाए
जैसे: शंकु + अर्धगोला, बेलन + गोला, ice-cream cone, गुलाबजामुन, खिलौना, etc.

📐 मुख्य सूत्र (याद रखें!):

1️⃣ शंकु (Cone):
आयतन = (1/3)πr²h

2️⃣ बेलन (Cylinder):
आयतन = πr²h

3️⃣ गोला (Sphere):
आयतन = (4/3)πr³

4️⃣ अर्धगोला (Hemisphere):
आयतन = (2/3)πr³ (गोले का आधा)

💡 संयुक्त आकृतियों का Pattern:

Type 1: शंकु + अर्धगोला (Ice-cream cone, खिलौना):
कुल आयतन = (1/3)πr²h + (2/3)πr³
= (1/3)πr²(h + 2r)

Type 2: बेलन + 2 अर्धगोले (गुलाबजामुन):
कुल आयतन = πr²h + 2×(2/3)πr³
= πr²h + (4/3)πr³
= πr²[h + 4r/3]

Q19 पहला भाग – शंकु + अर्धगोला:
r = 2 cm, शंकु की ऊंचाई = 2 cm

Step 1: खिलौने का आयतन
= (1/3)πr²h + (2/3)πr³
= (1/3) × 3.14 × 4 × 2 + (2/3) × 3.14 × 8
= (1/3) × 3.14 × 4 × (2 + 4)
= 25.12 cm³

Step 2: बेलन का आयतन (जिसमें fit हो सके)
H = शंकु की ऊंचाई + hemisphere की radius
H = 2 + 2 = 4 cm
= πr²H = 3.14 × 4 × 4 = 50.24 cm³

Step 3: अंतर = 50.24 – 25.12 = 25.12 cm³

Q19 दूसरा भाग (OR) – गुलाबजामुन (Capsule shape):
Length = 5 cm, diameter = 2.8 cm, r = 1.4 cm

Step 1: Cylindrical भाग की लंबाई
दोनों तरफ hemisphere है (radius = 1.4)
Cylinder length = 5 – 2r = 5 – 2.8 = 2.2 cm

Step 2: कुल आयतन
= πr²h + 2 × (2/3)πr³
= πr²[h + 4r/3]
= (22/7) × 1.96 × [2.2 + 1.867]
≈ 25.05 cm³

Step 3: 30% चाशनी
= 0.30 × 25.05 = 7.515 cm³ (per piece)
45 में = 45 × 7.515 = 338 cm³

💡 ऐसे प्रश्नों में Steps:
1. Identify करें कौन-कौन से shapes हैं
2. Common radius/dimension पहचानें
3. हर shape का आयतन अलग-अलग निकालें
4. जोड़ो या घटाओ (प्रश्न के अनुसार)
5. Percentage/multiplication apply करें (if needed)

परीक्षा में ध्यान दें:
1. Diagram ध्यान से देखें – कौन सा shape कहां है
2. Radius same है दोनों shapes में (usually)
3. Heights अलग-अलग पहचानें
4. Formula लिखें फिर substitute करें
5. π का मान प्रश्न में दिया होगा (22/7 या 3.14)
6. Units cube में (cm³, m³)

आम गलतियां जिनसे बचें:
❌ Hemisphere के लिए full sphere का formula लगा दिया
❌ Cylinder की height गलत ली (hemisphere की radius घटाना भूल गए)
❌ Radius और diameter confuse कर दिए
❌ दो अर्धगोले हैं लेकिन सिर्फ एक count किया
❌ Percentage/total count apply करना भूल गए

याद रखने की Trick:
“शंकु एक तिहाई, बेलन पूरा,
अर्धगोला दो तिहाई, गोला चार तिहाई सुरा”

Cone = (1/3)πr²h
Cylinder = πr²h (1 × πr²h)
Hemisphere = (2/3)πr³
Sphere = (4/3)πr³

💡 Real Life Examples:
• Ice-cream cone = Cone + Hemisphere
• गुलाबजामुन = Cylinder + 2 Hemispheres
• Rocket = Cone + Cylinder
• खिलौना = कई shapes का combination
• Capsule (medicine) = Cylinder + 2 Hemispheres

20. निम्न आंकड़ों का बहुलक ज्ञात करें:

परिवार का माप	1-3	3-5	5-7	7-9	9-11
परिवारों की संख्या	7	8	2	2	1

चरण 1: बहुलक वर्ग ज्ञात करना:
सबसे अधिक बारंबारता = 8
अतः बहुलक वर्ग = 3-5

चरण 2: बहुलक सूत्र:
Mode = l + [(f₁ – f₀) / (2f₁ – f₀ – f₂)] × h
जहाँ:
• l = 3 (निम्न सीमा)
• f₁ = 8 (बहुलक वर्ग की बारंबारता)
• f₀ = 7 (पूर्ववर्ती वर्ग की बारंबारता)
• f₂ = 2 (उत्तरवर्ती वर्ग की बारंबारता)
• h = 2 (वर्ग का आकार)

Mode = 3 + [(8 – 7) / (2×8 – 7 – 2)] × 2
= 3 + [1 / (16 – 9)] × 2
= 3 + (1/7) × 2
= 3 + 2/7
= 3 + 0.286
= 3.286

✅ बहुलक = 3.286

📖 बहुलक (Mode) – Grouped Data – बिल्कुल आसान भाषा में

⭐ बहुलक क्या है? (What is Mode?)

Simple Definition:
बहुलक वह मान है जो सबसे ज्यादा बार आता है।

Real Life Example:
• कक्षा में सबसे common shoe size = Mode
• सबसे ज्यादा बिकने वाला product = Mode
• परिवार में सबसे common size = Mode (यह प्रश्न!)

Grouped Data में:
जिस class में सबसे ज्यादा frequency हो = Modal Class
उसी class में Mode होता है।

📐 Mode Formula (Grouped Data):
Mode = l + [(f₁ – f₀)/(2f₁ – f₀ – f₂)] × h

जहां:
• l = Lower boundary (बहुलक वर्ग की निचली सीमा)
• f₁ = बहुलक वर्ग की frequency (सबसे बड़ी वाली)
• f₀ = पूर्ववर्ती वर्ग की frequency (पहले वाली class)
• f₂ = उत्तरवर्ती वर्ग की frequency (बाद वाली class)
• h = Class size (वर्ग का आकार)

📝 Step-by-Step Method (Q20 Example):

Step 1: Modal Class ढूंढो
सभी frequencies देखो: 7, 8, 2, 2, 1
सबसे बड़ी frequency = 8
∴ Modal Class = 3-5

Step 2: सभी values identify करो
• l = 3 (modal class की lower limit)
• f₁ = 8 (modal class की frequency)
• f₀ = 7 (पहले वाली class 1-3 की frequency)
• f₂ = 2 (बाद वाली class 5-7 की frequency)
• h = 5 – 3 = 2 (class size)

Step 3: Formula में डालो
Mode = 3 + [(8-7)/(2×8-7-2)] × 2
= 3 + [1/(16-9)] × 2
= 3 + (1/7) × 2
= 3 + 2/7
= 3.286

💡 Mean vs Median vs Mode – Difference:

1️⃣ Mean (माध्य):
• Average = सभी values का योग / संख्या
• सभी values को consider करता है
• Extreme values से affected होता है

2️⃣ Median (माध्यक):
• Middle value = बीच वाला मान
• आंकड़ों को arrange करके निकालते हैं
• Formula: l + [(N/2 – cf)/f] × h

3️⃣ Mode (बहुलक):
• Most frequent value = सबसे ज्यादा बार आने वाला
• Highest frequency वाली class में होता है
• Formula: l + [(f₁-f₀)/(2f₁-f₀-f₂)] × h

⚠️ Common Mistakes (Exam में ये गलतियां मत करना!):

❌ Mistake 1: Modal class = सबसे पहली या सबसे बड़ी class
✅ Correct: Modal class = highest frequency वाली class

❌ Mistake 2: f₀ और f₂ उल्टा लिखना
✅ Correct: f₀ = पहले वाली, f₂ = बाद वाली class की frequency

❌ Mistake 3: Formula में 2f₁ की जगह f₁ लिखना
✅ Correct: Denominator = 2f₁ – f₀ – f₂

❌ Mistake 4: h (class size) गलत निकालना
✅ Correct: h = Upper limit – Lower limit

❌ Mistake 5: Mean/Median का formula use करना
✅ Correct: Mode का अलग formula है!

याद रखने की Trick:
“सबसे बड़ी आवृत्ति जहाँ,
बहुलक वर्ग वहीं जान”

Formula याद करने का तरीका:
Mode = l + [(f₁ – f₀)/(2f₁ – f₀ – f₂)] × h

“1-0-2 Pattern”:
• Numerator: f₁ – f₀ (1 minus 0)
• Denominator: 2f₁ – f₀ – f₂ (2 times 1, minus 0, minus 2)

Exam Tip: पहले f₁ (सबसे बड़ी frequency) ढूंढो, फिर उसके आगे-पीछे की frequencies देखो!

अथवा / OR

20 (OR). एक सर्वेक्षण में 20 मोहल्लों के बारे में निम्न आंकड़े प्राप्त हुए:

परिवार माप	1—3	3—5	5—7	7—9	9—11
परिवारों की संख्या	7	8	2	2	1

इन आंकड़ों का बहुलक ज्ञात कीजिए।

यह प्रश्न उपरोक्त प्रश्न 20 के समान ही है।

✅ बहुलक = 3.286

🎓 शुभकामनाएं / Best Wishes! 🎓

परीक्षा में सफलता के लिए हार्दिक शुभकामनाएं!

तैयारकर्ता: Vivek Vyas

Basic Computer Instructor

निर्देशन: Shri Susheel Kumar Sharma (Principal)

🌐 gsssjethantri.in

Content │ Design │ Code ⚙️ by Bharat Choudhary (Lecturer)

माध्यमिक शिक्षा बोर्ड राजस्थान, अजमेरमॉडल प्रश्न पत्र 2026विषय: गणित (MATHS)कक्षा— 10

परीक्षा योजना (Examination Blueprint) – 2026

उद्देश्य हेतु अंकभार

प्रश्नों के प्रकार अनुसार अंकभार

अध्याय-वार अंकभार (Chapter-wise Weightage)

📝 हल सहित मॉडल प्रश्न-पत्र (Solved Paper)

खण्ड-अ (SECTION-A)

(बहुविकल्पीय प्रश्न एवं अतिलघुत्तरात्मक प्रश्न)

📖 अपरिमेय संख्या क्या होती है?

📖 HCF और LCM क्या होते हैं?

📖 बहुपद का शून्यक (Zero) क्या होता है?

📖 दो रेखाओं का व्यवहार – बिल्कुल आसान भाषा में

📖 सार्वअन्तर (Common Difference) – बिल्कुल आसान भाषा में

📖 प्रथम n धन पूर्णांकों का योग – बिल्कुल आसान भाषा में

📖 त्रिभुजों की समरूपता (Similar Triangles) – बिल्कुल आसान भाषा में

📖 निर्देशांक ज्यामिति (Coordinate Geometry) – दूरी की अवधारणा

📖 त्रिकोणमिति (Trigonometry) – बिल्कुल आसान भाषा में

📖 ऊंचाई और दूरी (Heights & Distances) – बिल्कुल आसान भाषा में

📖 स्पर्श रेखा (Tangent to Circle) – बिल्कुल आसान भाषा में

📖 स्पर्श रेखा + पाइथागोरस प्रमेय – बिल्कुल आसान भाषा में

📖 त्रिज्यखंड (Sector) का क्षेत्रफल – बिल्कुल आसान भाषा में

📖 अर्धगोला (Hemisphere) का पृष्ठीय क्षेत्रफल – बिल्कुल आसान भाषा में

📖 ठोस आकृतियों को जोड़ना – बिल्कुल आसान भाषा में

📖 बहुलक (Mode) – बिल्कुल आसान भाषा में

📖 माध्य, माध्यक, बहुलक का संबंध – बिल्कुल आसान भाषा में

📖 पूरक घटना (Complementary Events) – बिल्कुल आसान भाषा में

2. निम्नलिखित प्रश्नों (i से vi) में रिक्त स्थानों की पूर्ति कीजिए। Fill in the blanks in the following questions (i to vi).

📖 द्विघात समीकरण और विवेचक (Discriminant)

📖 समांतर श्रेढ़ी (Arithmetic Progression – AP) क्या है?

📖 थेल्स प्रमेय (Basic Proportionality Theorem) – बिल्कुल आसान भाषा में

📖 त्रिकोणमितीय सर्वसमिकाएं (Trigonometric Identities) – बिल्कुल आसान भाषा में

📖 वृत्त और स्पर्श रेखा की शब्दावली – बिल्कुल आसान भाषा में

📖 पासे की प्रायिकता (Dice Probability) – बिल्कुल आसान भाषा में

3. अतिलघुत्तरात्मक प्रश्न (i से xii) Very short answer type question (i to xii)

📖 HCF और LCM का संबंध – बिल्कुल आसान भाषा में

📖 अभाज्य गुणनखंड (Prime Factorization) – बिल्कुल आसान भाषा में

📖 शून्यकों से बहुपद बनाना – बिल्कुल आसान भाषा में

📖 दो रेखाओं की स्थिति – बिल्कुल आसान भाषा में

📖 AP में n वां पद निकालना – बिल्कुल आसान भाषा में

📖 समदूरस्थ बिंदु (Equidistant Point) – बिल्कुल आसान भाषा में

📖 त्रिकोणमितीय सर्वसमिकाओं का उपयोग – बिल्कुल आसान भाषा में

📖 बाह्य बिंदु से स्पर्श रेखाएं – बिल्कुल आसान भाषा में

📖 वृत्त के त्रिज्यखंड का क्षेत्रफल – बिल्कुल आसान भाषा में

📖 समबाहु त्रिभुजों की समरूपता – बिल्कुल आसान भाषा में

📖 स्पर्श रेखा की मूल बातें – बिल्कुल आसान भाषा में

खण्ड-ब (SECTION-B)

लघुत्तरात्मक प्रश्न (Short Answer Type Questions) – प्रत्येक 2 अंक

📖 शून्यक और गुणांकों का संबंध – बिल्कुल आसान भाषा में

📖 दो अंकों की संख्या वाले प्रश्न – बिल्कुल आसान भाषा में

📖 AP निर्धारित करना जब दो पद दिए हों – बिल्कुल आसान भाषा में

📖 थेल्स प्रमेय / आधारभूत समानुपातिकता प्रमेय (BPT) – बिल्कुल आसान भाषा में

📖 संरेखी बिंदु (Collinear Points) – बिल्कुल आसान भाषा में

📖 त्रिकोणमिति + पाइथागोरस प्रमेय – बिल्कुल आसान भाषा में

📖 वृत्त की स्पर्श रेखा और कोण सिद्ध करना – बिल्कुल आसान भाषा में

📖 त्रिज्यखंड का व्यावहारिक उपयोग (Practical Applications) – बिल्कुल आसान भाषा में

📖 वर्गीकृत आंकड़ों का माध्य (Mean of Grouped Data) – बिल्कुल आसान भाषा में

📖 प्रायिकता (Probability) – बिल्कुल आसान भाषा में

खण्ड-स (SECTION-C)

दीर्घ उत्तरीय प्रश्न (Long Answer Type Questions) – प्रत्येक 3 अंक

📖 क्रमागत संख्याओं वाले प्रश्न – बिल्कुल आसान भाषा में

📖 विभाजन सूत्र / Section Formula – बिल्कुल आसान भाषा में

📖 त्रिकोणमितीय सर्वसमिकाएं सिद्ध करना – बिल्कुल आसान भाषा में

📖 माध्यक (Median) – Grouped Data – बिल्कुल आसान भाषा में

खण्ड-द (SECTION-D)

निबंधात्मक प्रश्न (Essay Type Questions) – प्रत्येक 4 अंक

📖 ऊंचाई और दूरी (Heights & Distances) – बिल्कुल आसान भाषा में

📖 संयुक्त ठोस आकृतियों का आयतन – बिल्कुल आसान भाषा में

📖 बहुलक (Mode) – Grouped Data – बिल्कुल आसान भाषा में

🎓 शुभकामनाएं / Best Wishes! 🎓

4 Comments